Tiệm cận ngang của đồ thị hàm số \(y=\sqrt{4x^2-8x+5}+2x\) có phương trình là
| \(y=4\) | |
| \(y=-2\) | |
| \(y=2\) | |
| \(y=-4\) |
Chọn phương án C.
Dùng chức năng r, với \(x=-999999\) (\(-\infty\)).
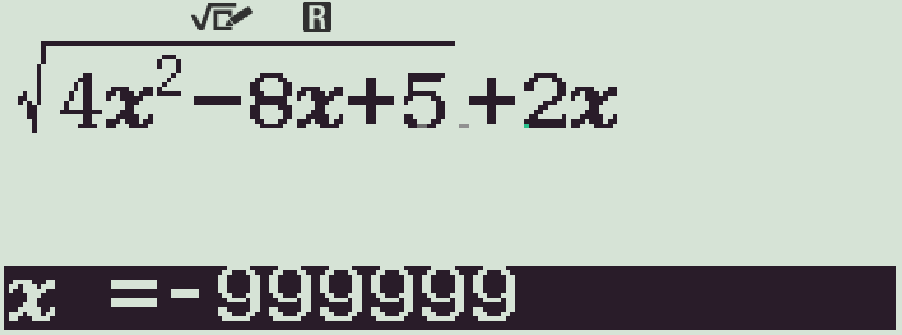
Ta được kết quả xấp xỉ \(2\)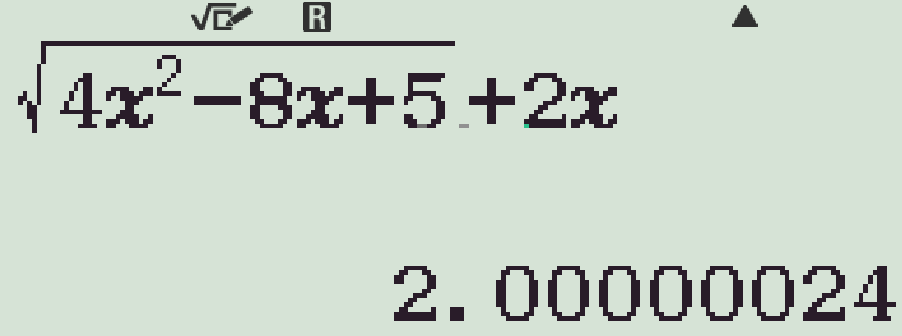
Vậy \(y=2\) là tiệm cận ngang.
Chọn phương án C.
\(\begin{aligned}
\lim\limits_{x\to-\infty}y&=\lim\limits_{x\to-\infty}\left(\sqrt{4x^2-8x+5}+2x\right)\\
&=\lim\limits_{x\to-\infty}\dfrac{\left(\sqrt{4x^2-8x+5}+2x\right)\left(\sqrt{4x^2-8x+5}-2x\right)}{\sqrt{4x^2-8x+5}-2x}\\
&=\lim\limits_{x\to-\infty}\dfrac{\left(4x^2-8x+5\right)-4x^2}{\sqrt{x^2\left(4-\dfrac{8}{x}+\dfrac{5}{x^2}\right)}-2x}\\
&=\lim\limits_{x\to-\infty}\dfrac{-8x+5}{|x|\sqrt{4-\dfrac{8}{x}+\dfrac{5}{x^2}}-2x}\\
&=\lim\limits_{x\to-\infty}\dfrac{-x\left(8-\dfrac{5}{x}\right)}{-x\sqrt{4-\dfrac{8}{x}+\dfrac{5}{x^2}}-2x}\\
&=\lim\limits_{x\to-\infty}\dfrac{-x\left(8-\dfrac{5}{x}\right)}{-x\left(\sqrt{4-\dfrac{8}{x}+\dfrac{5}{x^2}}+2\right)}\\
&=\lim\limits_{x\to-\infty}\dfrac{8-\dfrac{5}{x}}{\sqrt{4-\dfrac{8}{x}+\dfrac{5}{x^2}}+2}\\
&=\dfrac{8-0}{\sqrt{4-0+0}+2}=2.
\end{aligned}\)
Vậy \(y=2\) là tiệm cận ngang của đồ thị hàm số.
