Ngân hàng bài tập
A
Số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\sqrt{x+1}-1}{x^3-4x}\) lần lượt là
| \(3\) và \(1\) | |
| \(1\) và \(1\) | |
| \(2\) và \(1\) | |
| \(1\) và \(0\) |
2 lời giải
Chọn phương án B.
Dùng máy tính cầm tay:
- Dùng chức năng r, với \(x=999999\) (\(x\to+\infty\))
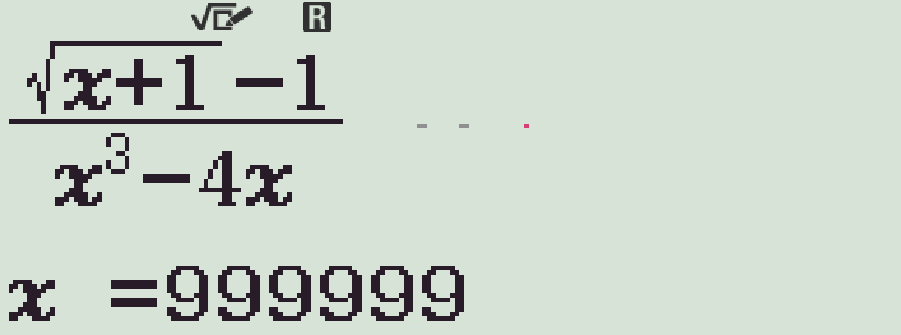
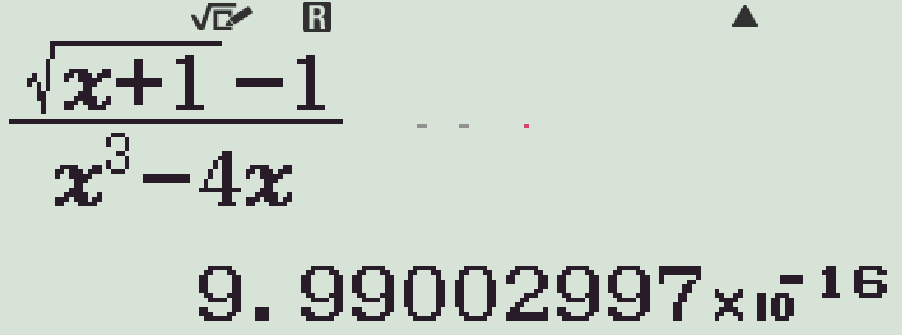
Vậy \(y=0\) là tiệm cận ngang. - Lại r, với \(x=1.999\) (\(x\to2^-\))
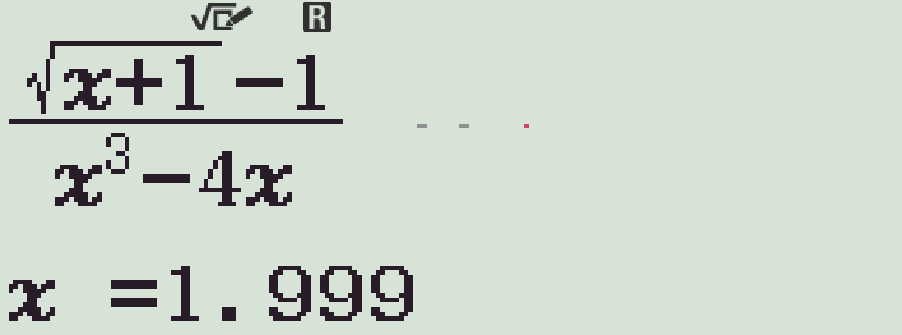

Vậy \(x=2\) là tiệm cận đứng.
Chọn phương án B.
\(\begin{aligned}
y&=\dfrac{\sqrt{x+1}-1}{x^3-4x}\\
&=\dfrac{\left(\sqrt{x+1}-1\right)\left(\sqrt{x+1}+1\right)}{x\left(x^2-4\right)\left(\sqrt{x+1}+1\right)}\\
&=\dfrac{x}{x\left(x^2-4\right)\left(\sqrt{x+1}+1\right)}\\
&=\dfrac{1}{\left(x^2-4\right)\left(\sqrt{x+1}+1\right)}
\end{aligned}\)
- \(\lim\limits_{x\to+\infty}\dfrac{1}{\left(x^2-4\right)\left(\sqrt{x+1}+1\right)}=0\)
Vậy \(y=0\) là tiệm cận ngang. - \(\lim\limits_{x\to2^-}\dfrac{1}{\left(x^2-4\right)\left(\sqrt{x+1}+1\right)}=-\infty\)
Vậy \(x=2\) là tiệm cận đứng.
