Ngân hàng bài tập
B
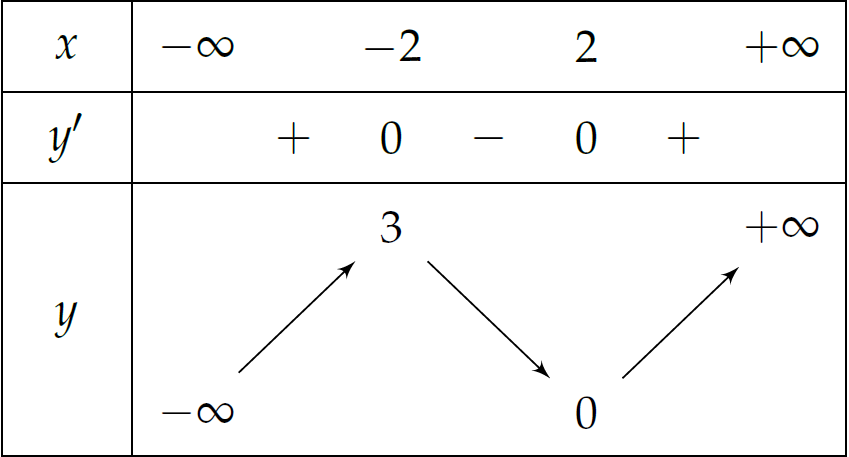
Cho hàm số \(y=f(x)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình trên. Số nghiệm thực của phương trình \(f(x)=1\) bằng
| \(2\) | |
| \(3\) | |
| \(1\) | |
| \(0\) |
1 lời giải
Chọn phương án B.
Đường thẳng \(y=1\) cắt đồ thị hàm số đã cho tại \(3\) điểm phân biệt.
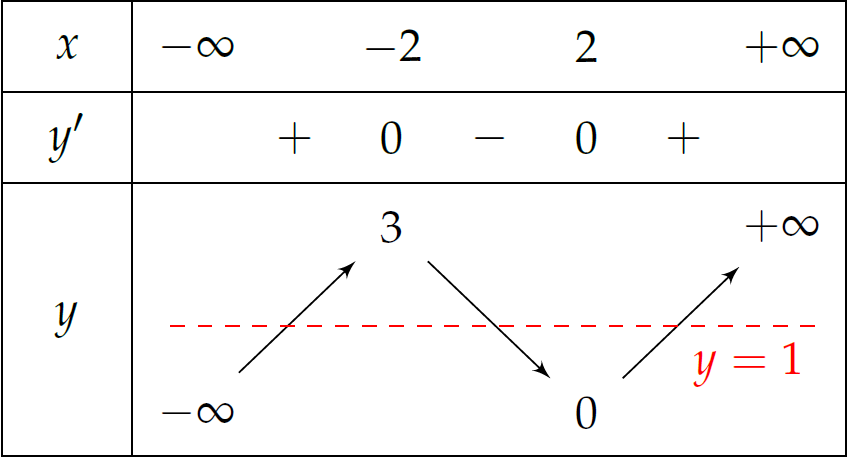
Suy ra phương trình \(f(x)=1\) có \(3\) nghiệm thực phân biệt.
