Ngân hàng bài tập
A
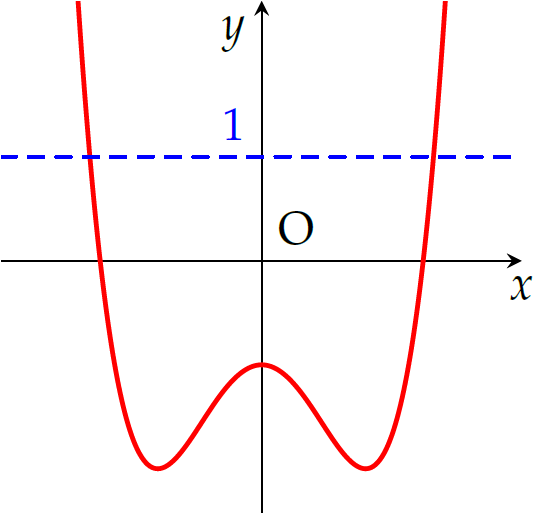
Đường cong ở hình trên là đồ thị của hàm số \(f(x)=ax^4+bx^2+c\); với \(x\) là biến số thực; \(a,\,b,\,c\) là ba hằng số thực, \(a\neq0\). Gọi \(k\) là số nghiệm thực của phương trình \(f(x)=1\). Mệnh đề nào dưới đây đúng?
| \(abc<0\) và \(k=2\) | |
| \(abc>0\) và \(k=3\) | |
| \(abc<0\) và \(k=0\) | |
| \(abc>0\) và \(k=2\) |
1 lời giải
Chọn phương án D.
- Quan sát đồ thị ta thấy \(a>0\).
- Vì đồ thị cắt trục tung tại điểm nằm phía dưới trục hoành nên suy ra \(c<0\).
- \(y'=4ax^3+2bx=2x(2a^2+b)\).
Từ hình vẽ ta thấy đồ thị có \(3\) điểm cực trị, do đó phương trình \(2ax^2+b=0\) có \(2\) nghiệm phân biệt, tức là \(b<0\).
Vậy \(abc>0\).
Mặt khác, vì đường thẳng \(y=1\) cắt đồ thị tại \(2\) điểm phân biệt nên phương trình \(f(x)=1\) có \(2\) nghiệm thực phân biệt.