Ngân hàng bài tập
A
Tính \(T=15+20+25+\cdots+7515\).
| \(T=5651265\) | |
| \(T=5651256\) | |
| \(T=5651625\) | |
| \(T=5651526\) |
2 lời giải
Chọn phương án A.
\(T\) là tổng của dãy số có số hạng tổng quát \(u_n=5(n+2)\).
Mặt khác \(7515=5(1501+2)\).
Vậy \(T=\displaystyle\sum_{n=1}^{1501}5(n+2)=5651265\).
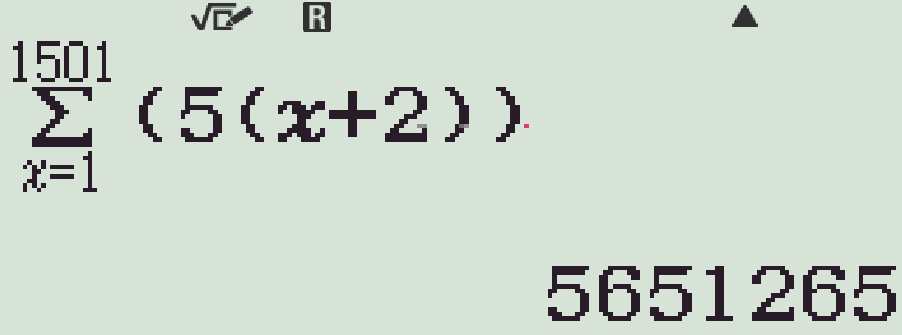
Chọn phương án A.
\(T\) là tổng của cấp số cộng có \(\begin{cases}
u_1=15\\
d=5\\
u_n=7515
\end{cases}\). Khi đó $$\begin{eqnarray*}
&u_1+(n-1)d&=7515\\
\Leftrightarrow&15+5(n-1)&=7515\\
\Leftrightarrow&5n+10&=7515\\
\Leftrightarrow&n&=1501.
\end{eqnarray*}$$
\(\begin{aligned}\Rightarrow T=S_{1501}&=\dfrac{1501}{2}\left(15+7515\right)\\
&=5651265.\end{aligned}\)
