Ngân hàng bài tập
SS
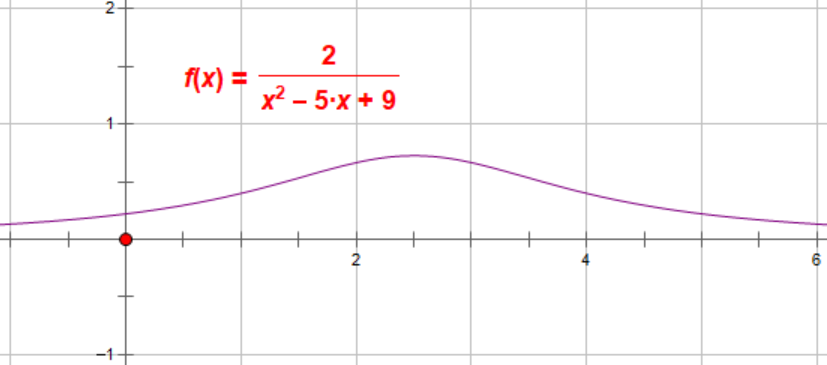
Giá trị lớn nhất của hàm số \(f(x)=\dfrac{2}{x^2-5x+9}\) bằng
| \(\dfrac{11}{8}\) | |
| \(\dfrac{11}{4}\) | |
| \(\dfrac{4}{11}\) | |
| \(\dfrac{8}{11}\) |
1 lời giải
Chọn phương án D.
\(\begin{aligned}x^2-5x+9&=x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}+9-\dfrac{25}{4}\\
&=\left(x-\dfrac{5}{2}\right)^2+\dfrac{11}{4}\geq\dfrac{11}{4},\,\forall x\in\Bbb{R}.\end{aligned}\)
Suy ra \(\dfrac{2}{x^2-5x+9}\leq\dfrac{2}{\tfrac{11}{4}}\Leftrightarrow f(x)\leq\dfrac{8}{11}\).
Vậy giá trị lớn nhất của \(f(x)\) là \(\dfrac{8}{11}\).