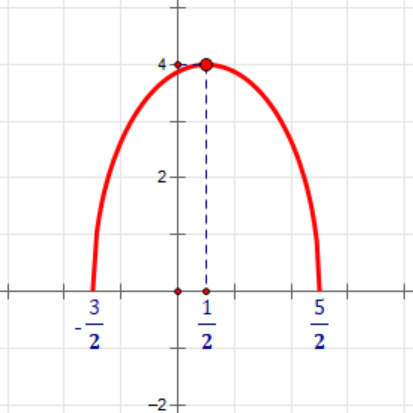
Giá trị lớn nhất của hàm số \(f(x)=\sqrt{(2x+3)(5-2x)}\) trên đoạn \(\left[-\dfrac{3}{2};\dfrac{5}{2}\right]\) là
| \(2\) | |
| \(4\) | |
| \(8\) | |
| \(2\sqrt{2}\) |
Chọn phương án B.
Ta có thể kiểm tra giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[-\dfrac{3}{2};\dfrac{5}{2}\right]\) bằng chức năng TABLE trên máy tính cầm tay.
Bước 1. Nhập hàm số \(f(x)\).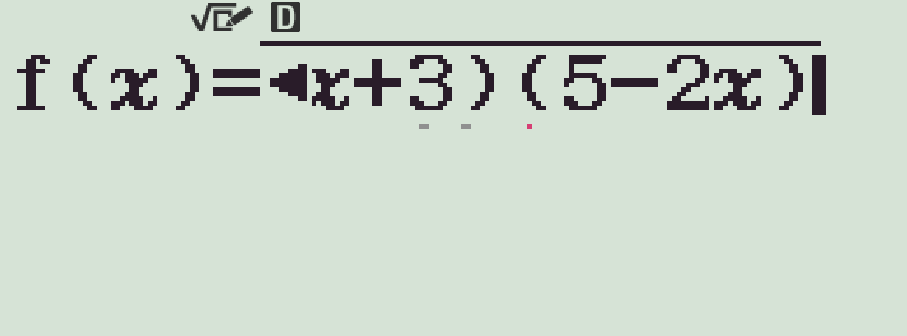
Bước 2. Chọn điểm bắt đầu (Start), kết thúc (End) và bước nhảy (Step).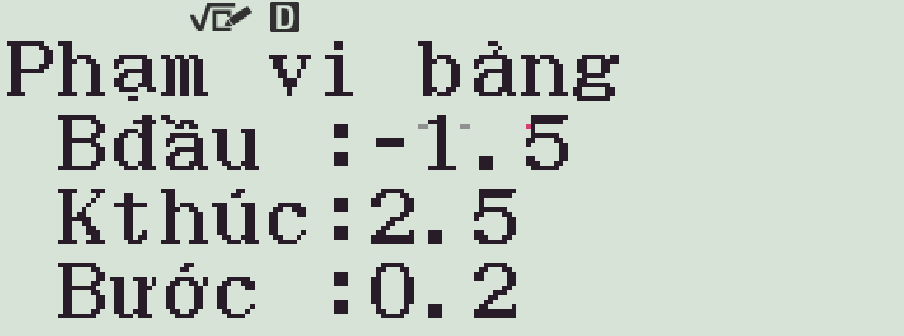
Bước 3. Quan sát giá trị của \(f(x)\), chọn giá trị lớn nhất (có thể chỉ gần đúng).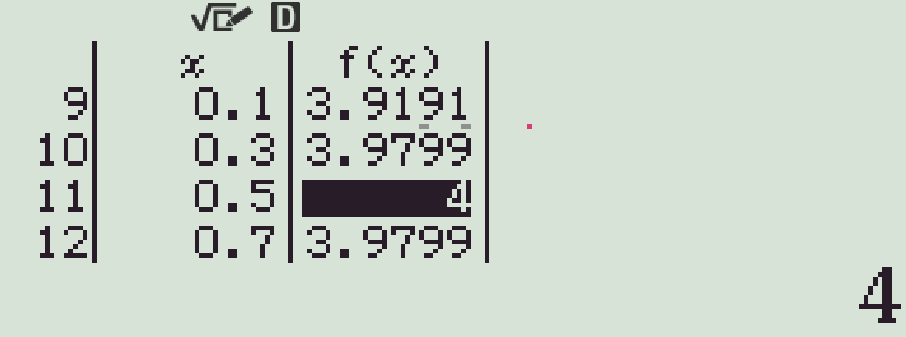
Chọn phương án B.
Áp dụng bất đẳng thức Cauchy cho hai số dương \(2x+3\) và \(5-2x\) ta có $$\begin{eqnarray*}
&\sqrt{(2x+3)(5-2x)}&\leq\dfrac{(2x+3)+(5-2x)}{2}\\
\Leftrightarrow&f(x)&\leq4
\end{eqnarray*}$$
Vậy giá trị lớn nhất của hàm số \(f(x)=\sqrt{(2x+3)(5-2x)}\) trên đoạn \(\left[-\dfrac{3}{2};\dfrac{5}{2}\right]\) là \(4\).