Ngân hàng bài tập
B
Cho tích phân \(I=\displaystyle\int_0^4x\sqrt{x^2+9}\mathrm{\,d}x\). Khi đặt \(t=\sqrt{x^2+9}\) thì tích phân đã cho trở thành
| \(I=\displaystyle\int_3^5t\mathrm{\,d}t\) | |
| \(I=\displaystyle\int_0^4t\mathrm{\,d}t\) | |
| \(I=\displaystyle\int_0^4t^2\mathrm{\,d}t\) | |
| \(I=\displaystyle\int_3^5t^2\mathrm{\,d}t\) |
2 lời giải
Chọn phương án D.
Dùng máy tính cầm tay:
- Ta có
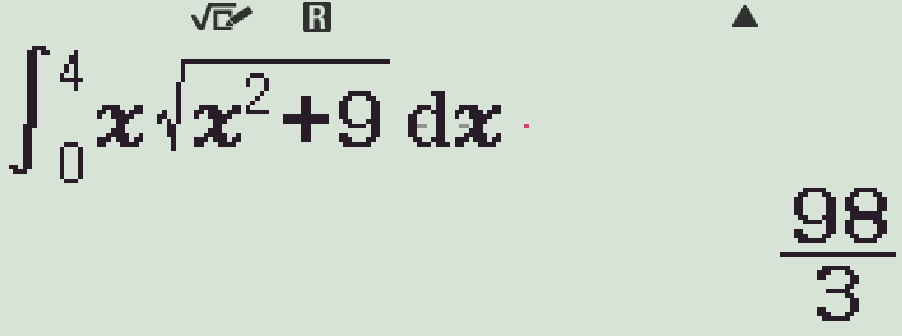
- Kiểm tra từng phương án, ta thấy

Chọn phương án D.
Với \(t=\sqrt{x^2+9}\) ta có
- \(t^2=x^{2}+9\Rightarrow t\mathrm{\,d}t=x\mathrm{\,d}x\).
- \(x=0\Rightarrow t=3\)
- \(x=4\Rightarrow t=5\).
Khi đó \(I=\displaystyle\int_0^4\sqrt{x^2+9}\cdot x\mathrm{\,d}x=\displaystyle\int_3^5t^2\mathrm{\,d}t\).
