Ngân hàng bài tập
A
Tập nghiệm của bất phương trình $$x^2+\left(\sqrt{3}+\sqrt{2}\right)x+\sqrt{6}\leq0$$là đoạn \([m;n]\). Tính \(m^2-n^2\).
| \(m^2-n^2=\sqrt{3}-\sqrt{2}\) | |
| \(m^2-n^2=\sqrt{2}-\sqrt{3}\) | |
| \(m^2-n^2=1\) | |
| \(m^2-n^2=-1\) |
1 lời giải
Chọn phương án C.
\(x^2+\left(\sqrt{3}+\sqrt{2}\right)x+\sqrt{6}=0\Leftrightarrow\left[\begin{array}{l}x=-\sqrt{3}\\ x=-\sqrt{2}\end{array}\right.\)
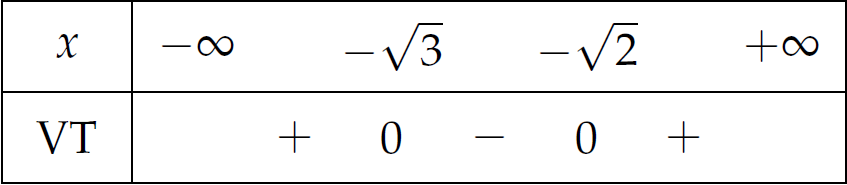
Vậy tập nghiệm của bất phương trình đã cho là đoạn \(\left[-\sqrt{3};-\sqrt{2}\right]\).
Suy ra \(\begin{cases}
m=-\sqrt{3}\\ n=-\sqrt{2}
\end{cases}\Rightarrow m^2-n^2=1\).
