Ngân hàng bài tập
C
Kết quả của giới hạn \(\lim\dfrac{3\sin n+4\cos n}{n+1}\) bằng
| \(1\) | |
| \(0\) | |
| \(2\) | |
| \(3\) |
2 lời giải
Chọn phương án B.
Dùng máy tính cầm tay:
- Dùng chức năng r, với \(x=999999\)
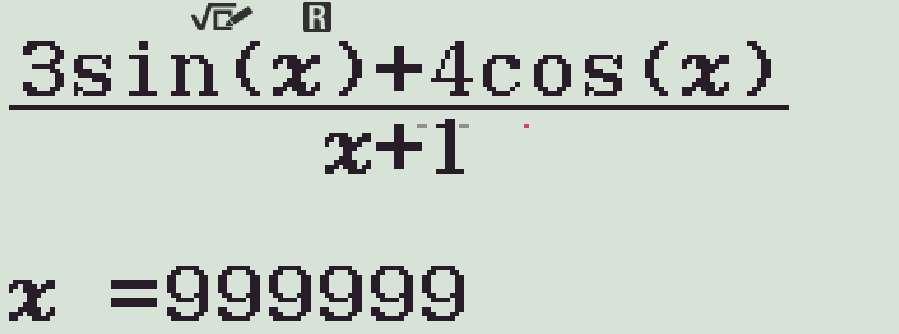
- Kết quả có phần đuôi \(\times10^{-6}\) cho thấy giới hạn đã cho bằng \(0\)
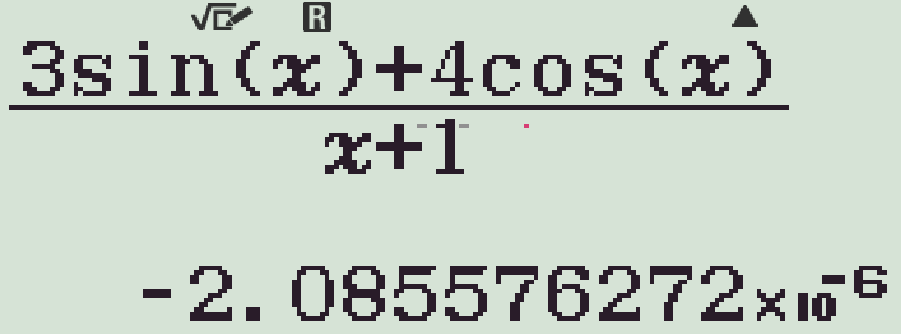
Chọn phương án B.
Ta có \(0\leq\left|\dfrac{\sin n}{n+1}\right|\leq\dfrac{1}{n+1}\) và \(0\leq\left|\dfrac{\cos n}{n+1}\right|\leq\dfrac{1}{n+1}\).
Mà \(\lim\dfrac{1}{n+1}=0\).
Suy ra \(\lim\dfrac{\sin n}{n+1}=\lim\dfrac{\cos n}{n+1}=0\).
Do đó $$\lim\dfrac{3\sin n+4\cos n}{n+1}=3\lim\dfrac{\sin n}{n+1}+4\lim\dfrac{\cos n}{n+1}=0.$$
