Ngân hàng bài tập
SS
Tìm tất cả các giá trị của tham số \(a\) để $$\lim\dfrac{5n^2-3an^4}{(1-a)n^4+2n+1}>0$$
| \(\left[\begin{array}{l}a\leq0\\ a\geq1\end{array}\right.\) | |
| \(0< a<1\) | |
| \(\left[\begin{array}{l}a<0\\ a>1\end{array}\right.\) | |
| \(0\leq a<1\) |
1 lời giải
Chọn phương án C.
\(\begin{aligned}
\lim\dfrac{5n^2-3an^4}{(1-a)n^4+2n+1}&=\lim\dfrac{\dfrac{5}{n^2}-3a}{1-a+\dfrac{2}{n^3}+\dfrac{1}{n^4}}\\
&=\dfrac{0-3a}{1-a+0+0}\\
&=\dfrac{-3a}{1-a}.
\end{aligned}\)
Theo yêu cầu đề bài, ta có bất phương trình \(\dfrac{-3a}{1-a}>0\).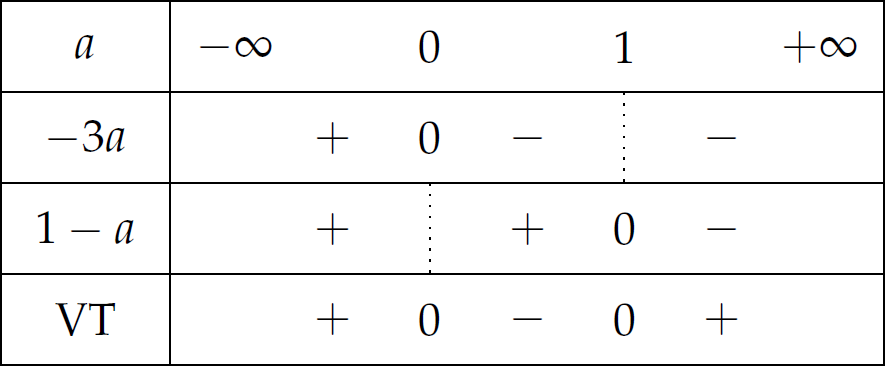
Suy ra \(\left[\begin{array}{l}a<0\\ a>1.\end{array}\right.\)
