Ngân hàng bài tập
B
Tính giới hạn \(\lim\dfrac{2-5^{n+2}}{3^n+2\cdot5^n}\).
| \(-\dfrac{25}{2}\) | |
| \(\dfrac{5}{2}\) | |
| \(1\) | |
| \(-\dfrac{5}{2}\) |
2 lời giải
Chọn phương án A.
Dùng máy tính cầm tay:
- Dùng chức năng r, với \(x=99\)
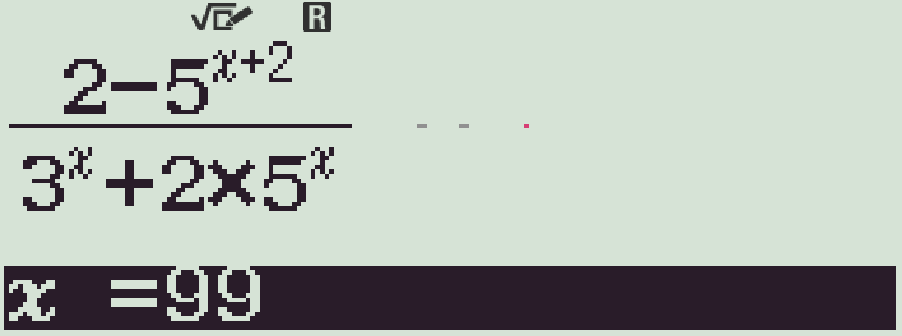
- Kết quả xấp xỉ \(-\dfrac{25}{2}\)
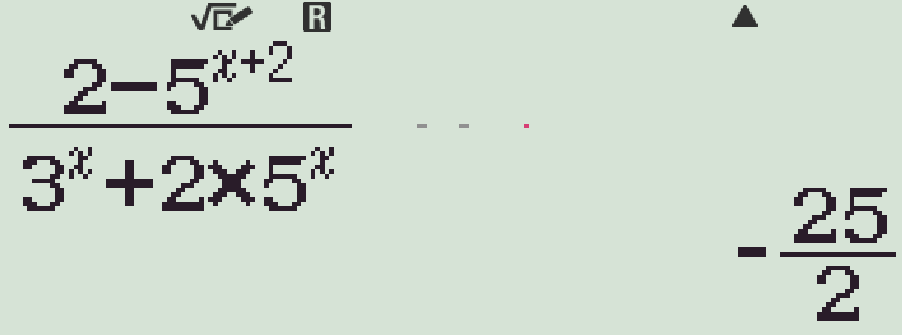
Chọn phương án A.
\(\begin{aligned}
\lim\dfrac{2-5^{n+2}}{3^n+2\cdot5^n}&=\lim\dfrac{2-5^2\cdot5^n}{3^n+2\cdot5^n}\\
&=\lim\dfrac{\dfrac{2}{5^n}-5^2}{\dfrac{3^n}{5^n}+2}\\
&=\lim\dfrac{2\cdot\left(\dfrac{1}{5}\right)^n-25}{\left(\dfrac{3}{5}\right)^n+2}\\
&=\dfrac{2\cdot0-25}{0+2}=-\dfrac{25}{2}.
\end{aligned}\)
Nếu \(q\in(-1;1)\) thì \(\lim q^n=0\)
