Tính \(L=\lim\left(\sqrt[3]{n^2-n^3}+n\right)\).
| \(\dfrac{1}{3}\) | |
| \(+\infty\) | |
| \(0\) | |
| \(1\) |
Chọn phương án A.
Dùng máy tính cầm tay:
- Dùng chức năng r, với \(x=999999\)
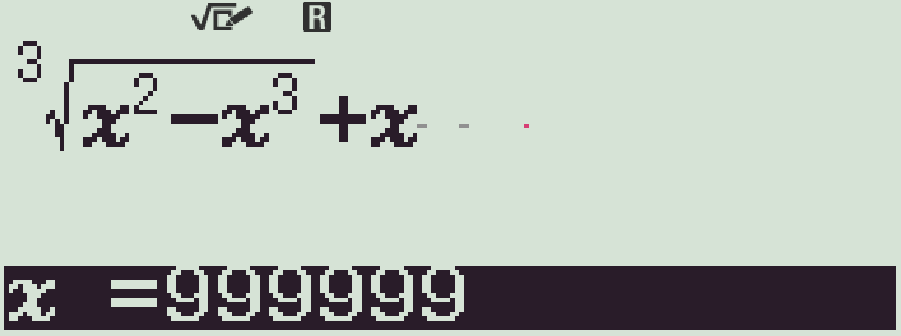
- Kết quả xấp xỉ \(\dfrac{1}{3}\)
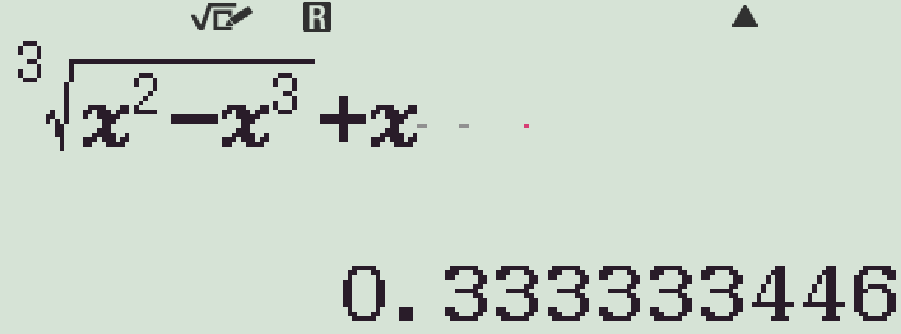
Chọn phương án A.
\(\begin{aligned}
L&=\lim\left(\sqrt[3]{n^2-n^3}+n\right)\\
&=\lim\dfrac{\left(\sqrt[3]{n^2-n^3}+n\right)\left(\sqrt[3]{\left(n^2-n^3\right)^2}-n\sqrt[3]{n^2-n^3}+n^2\right)}{\sqrt[3]{\left(n^2-n^3\right)^2}-n\sqrt[3]{n^2-n^3}+n^2}\\
&=\lim\dfrac{\left(n^2-n^3\right)+n^3}{\sqrt[3]{n^4-2n^5+n^6}-n\sqrt[3]{n^3\left(\dfrac{1}{n}-1\right)}+n^2}\\
&=\lim\dfrac{n^2}{\sqrt[3]{n^6\left(\dfrac{1}{n^2}-\dfrac{2}{n}+1\right)}-n^2\sqrt[3]{\dfrac{1}{n}-1}+n^2}\\
&=\lim\dfrac{n^2}{n^2\sqrt[3]{\dfrac{1}{n^2}-\dfrac{2}{n}+1}-n^2\sqrt[3]{\dfrac{1}{n}-1}+n^2}\\
&=\lim\dfrac{1}{\sqrt[3]{\dfrac{1}{n^2}-\dfrac{2}{n}+1}-\sqrt[3]{\dfrac{1}{n}-1}+1}\\
&=\dfrac{1}{\sqrt[3]{0-0+1}-\sqrt[3]{0-1}+1}=\dfrac{1}{3}.
\end{aligned}\)
