Ngân hàng bài tập
A
Cho góc \(\alpha\) thỏa mãn \(\tan\alpha=5\). Tính $$P=\sin^4\alpha-\cos^4\alpha.$$
| \(P=\dfrac{9}{13}\) | |
| \(P=\dfrac{10}{13}\) | |
| \(P=\dfrac{11}{13}\) | |
| \(P=\dfrac{12}{13}\) |
2 lời giải
Chọn phương án D.
Dùng máy tính cầm tay:
- Bấm ql?5)=

- Bấm \(\sin(\)M\()^4-\cos(\)M\()^4\)=
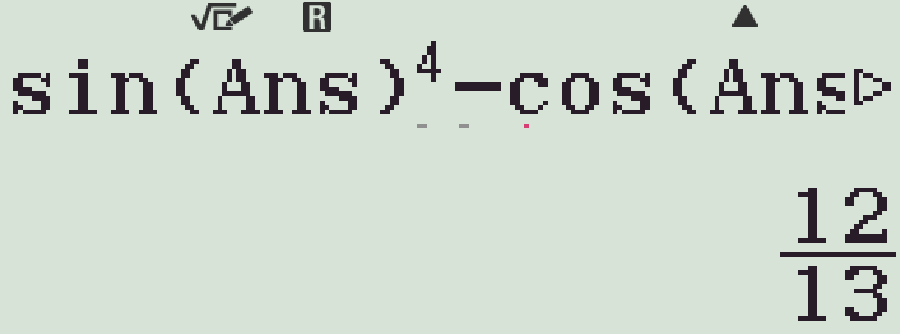
Chọn phương án D.
Ta có \(\dfrac{1}{\cos^2\alpha}=1+\tan^2\alpha=1+25=26\).
Suy ra \(\cos^2\alpha=\dfrac{1}{26}\).
Khi đó $$\begin{aligned}
P&=\sin^4\alpha-\cos^4\alpha\\
&=\left(\sin^2\alpha\right)^2-\left(\cos^2\alpha\right)^2\\
&=\left(\sin^2\alpha+\cos^2\alpha\right)\left(\sin^2\alpha-\cos^2\alpha\right)\\
&=1\cdot\left(\sin^2\alpha-\cos^2\alpha\right)\\
&=\sin^2\alpha-\cos^2\alpha.\\
&=\left(1-\cos^2\alpha\right)-\cos^2\alpha\\
&=1-2\cos^2\alpha\\
&=1-2\cdot\dfrac{1}{26}=\dfrac{12}{13}.
\end{aligned}$$
