Tổng tất cả các nghiệm nguyên của hệ bất phương trình \(\begin{cases}
5x-2<4x+5\\
x^2<(x+2)^2
\end{cases}\) bằng
| \(21\) | |
| \(28\) | |
| \(27\) | |
| \(29\) |
Chọn phương án A.
Ta có $\begin{cases}5x-2<4x+5\\ x^2<(x+2)^2\end{cases}\Leftrightarrow\begin{cases} 5x-2-(4x+5)<0\\ x^2-(x+2)^2<0.\end{cases}$
Ta tìm các số nguyên $x$ thỏa mãn hệ trên thông qua chức năng TABLE của máy tính cầm tay (chế độ 2 hàm $f(x)$ và $g(x)$).
- Nhập hàm $f(x)=5x-2-(4x+5)$.
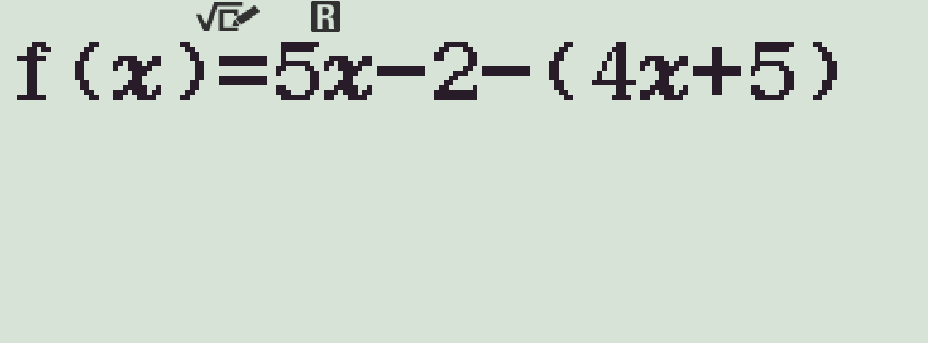
- Nhập hàm $g(x)=x^2-(x+2)^2$.

- Ta khảo sát trên đoạn $[-10;10]$ với bước nhảy Step=1.
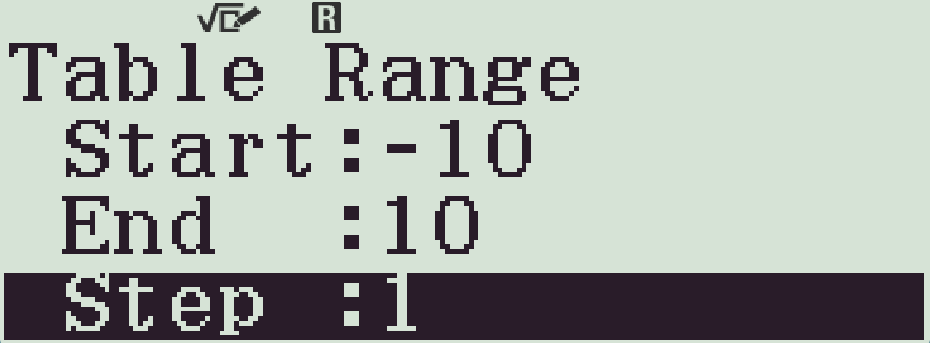
- Ta cần tìm những giá trị $x$ sao cho đồng thời $f(x)<0$ và $g(x)<0$.
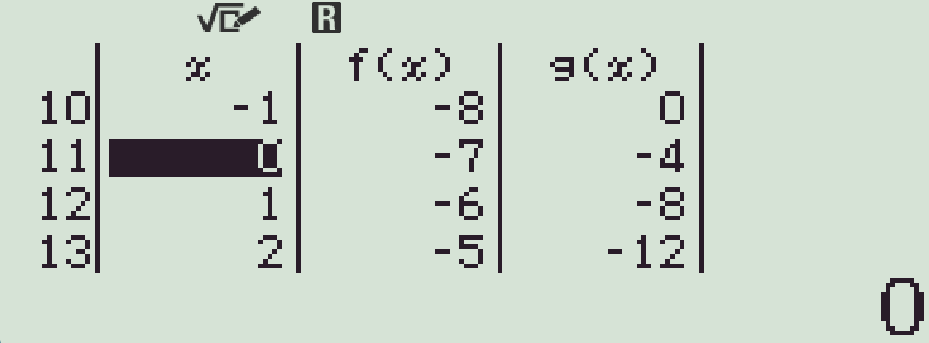
Theo đó, ta tìm được $7$ số nguyên $x\in\{0;1;2;3;4;5;6\}$.
Vậy tổng tất cả các nghiệm nguyên là $0+1+2+3+4+5+6=21$.
Chọn phương án A.
\(\begin{aligned}
\blacksquare&\,5x-2<4x+5\\
\Leftrightarrow&\,x<7\,\,(1)\\
\blacksquare&\,x^2<(x+2)^2\\
\Leftrightarrow&\,(x+2)^2-x^2>0\\
\Leftrightarrow&\,(x+2-x)(x+2+x)>0\\
\Leftrightarrow&\,2(2x+2)>0\\
\Leftrightarrow&\,x>-1\,\,(2)
\end{aligned}\)
Từ (1) và (2) suy ra \(S=(-1;7)\).
Vậy tổng tất cả các nghiệm nguyên là \(0+1+2+3+4+5+6=21\).
