Cho góc \(\alpha\) thỏa mãn \(\sin\alpha\cdot\cos\alpha=\dfrac{12}{25}\) và \(\sin\alpha+\cos\alpha>0\). Tính $$P=\sin^3\alpha+\cos^3\alpha$$
| \(P=\dfrac{91}{125}\) | |
| \(P=\dfrac{49}{25}\) | |
| \(P=\dfrac{7}{5}\) | |
| \(P=\dfrac{1}{9}\) |
Chọn phương án A.
Dùng máy tính cầm tay:
- Nhập \(\sin(x)\times\cos(x)\)Qr(=)\(\dfrac{12}{25}\)
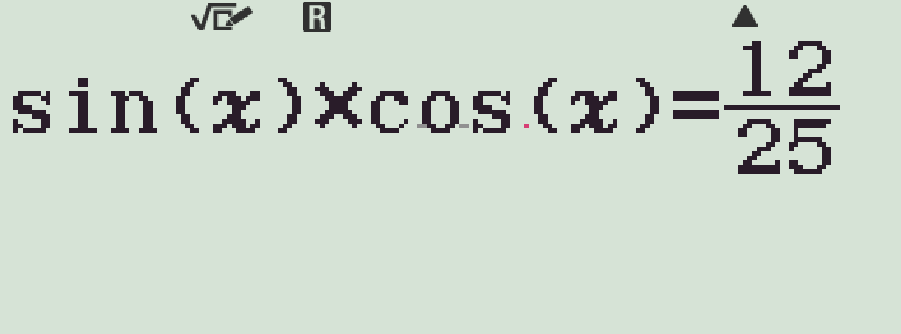
- Bấm qr(SOLVE), với \(x=0\) (rad)
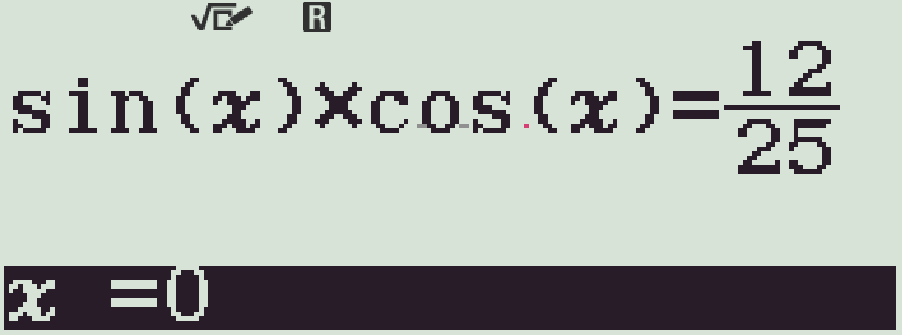
ta được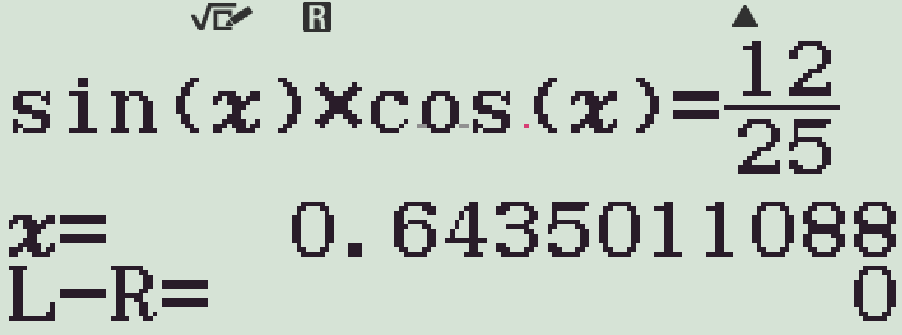
- Lưu kết quả này vào biến nhớ A
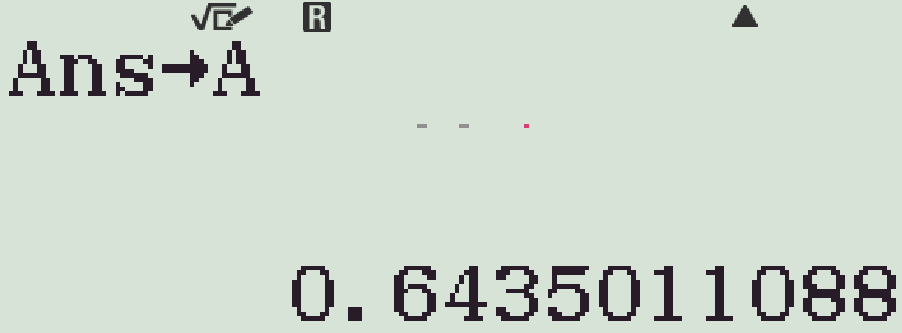
- Bấm \(\sin(A)^3+\cos(A)^3\)=
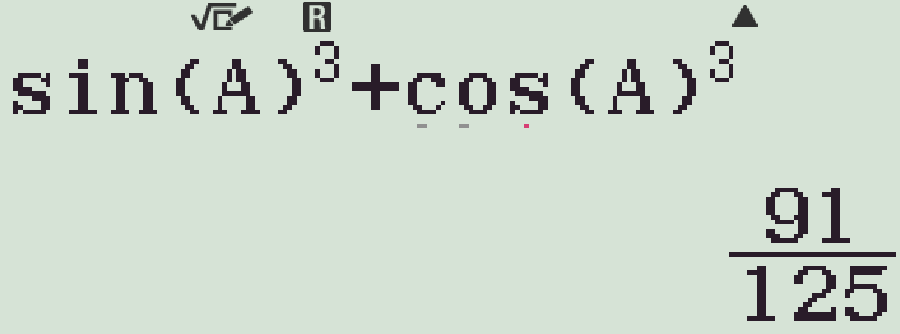
Chọn phương án A.
\(\begin{aligned}
\left(\sin\alpha+\cos\alpha\right)^2&=\sin^2\alpha+2\sin\alpha\cdot\cos\alpha+\cos^2\alpha\\
&=\left(\sin^2\alpha+\cos^2\alpha\right)+2\sin\alpha\cdot\cos\alpha\\
&=1+2\sin\alpha\cdot\cos\alpha\\
&=1+2\cdot\dfrac{12}{25}=\dfrac{49}{25}.
\end{aligned}\)
Vì \(\sin\alpha+\cos\alpha>0\) nên $$\sin\alpha+\cos\alpha=\dfrac{7}{5}.$$
Khi đó ta có $$\begin{aligned}
P&=\sin^3\alpha+\cos^3\alpha\\
&=\left(\sin\alpha+\cos\alpha\right)\left(\sin^2\alpha-\sin\alpha\cdot\cos\alpha+\cos^2\alpha\right)\\
&=\left(\sin\alpha+\cos\alpha\right)\left(\sin^2\alpha+\cos^2\alpha-\sin\alpha\cdot\cos\alpha\right)\\
&=\left(\sin\alpha+\cos\alpha\right)\left(1-\sin\alpha\cdot\cos\alpha\right)\\
&=\dfrac{7}{5}\left(1-\dfrac{12}{25}\right)=\dfrac{91}{125}.
\end{aligned}$$
