Ngân hàng bài tập
S
Cho góc \(\alpha\) thỏa mãn \(\tan\alpha+\cot\alpha=2\). Tính $$P=\tan^2\alpha+\cot^2\alpha$$
| \(P=1\) | |
| \(P=2\) | |
| \(P=3\) | |
| \(P=4\) |
2 lời giải
Chọn phương án B.
Dùng máy tính cầm tay:
- Nhập \(\tan(x)+\dfrac{1}{\tan(x)}\)Qr(=)\(2\)
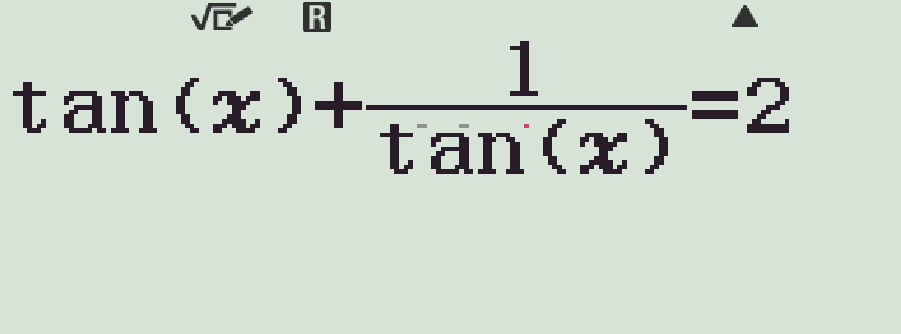
- Bấm qr(SOLVE), với \(x=0\) (rad)
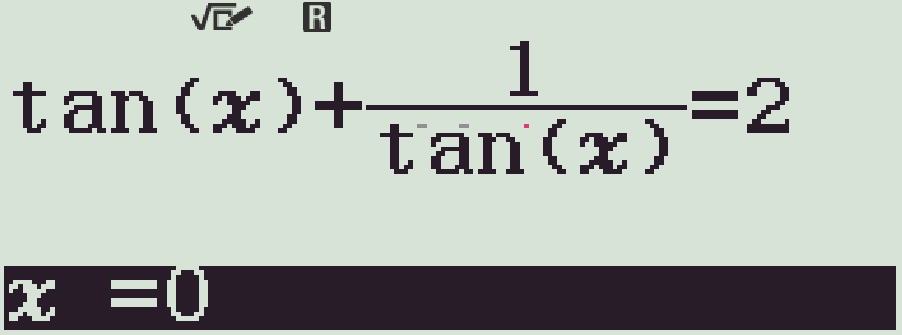
ta được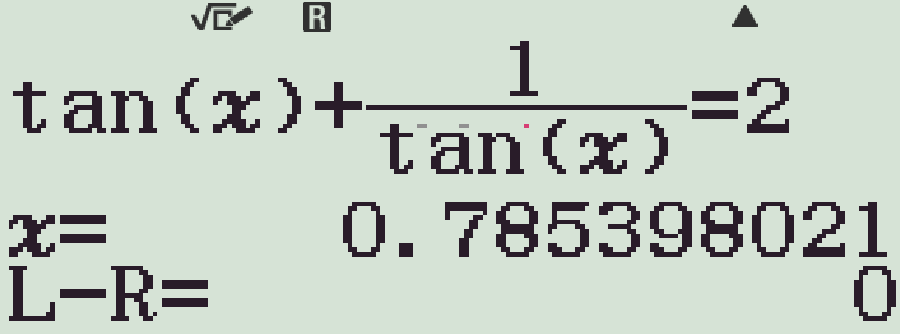
- Lưu kết quả này vào biến nhớ A

- Bấm \(\tan(A)^2+\dfrac{1}{\tan(A)^2}\)=
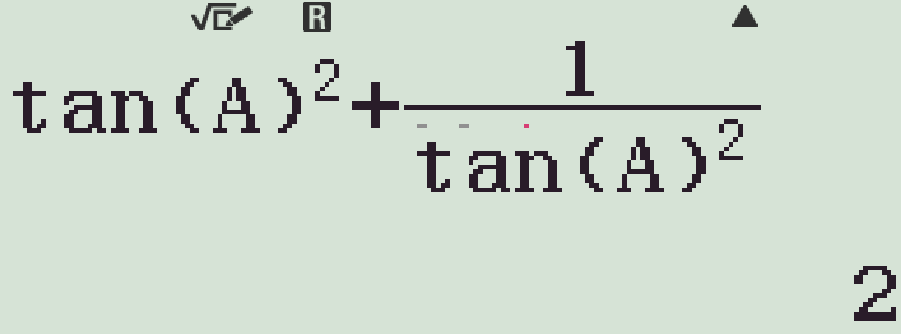
Chọn phương án B.
\(\begin{eqnarray*}
&\left(\tan\alpha+\cot\alpha\right)^2&=\tan^2\alpha+2\tan\alpha\cdot\cot\alpha+\cot^2\alpha\\
\Leftrightarrow&2^2&=\tan^2\alpha+\cot^2\alpha+2\cdot1\\
\Leftrightarrow&2&=P.
\end{eqnarray*}\)
