Ngân hàng bài tập
A
Rút gọn biểu thức \(M=\tan^2x-\sin^2x\).
| \(M=\tan^2x\) | |
| \(M=\sin^2x\) | |
| \(M=\tan^2x\cdot\sin^2x\) | |
| \(M=1\) |
2 lời giải
Chọn phương án C.
Dùng máy tính cầm tay:
- Dùng chức năng r, với \(x=1\) (rad)
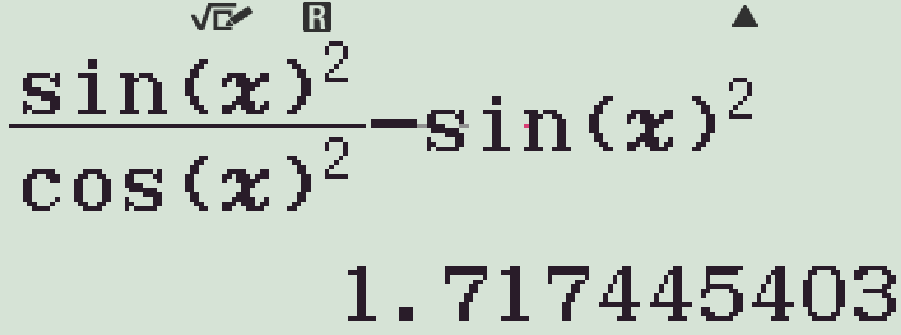
- Bấm tương tự cho từng phương án ta thấy
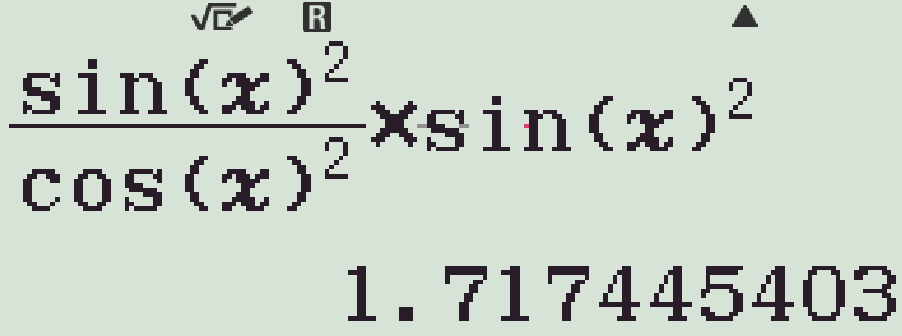
Vậy \(M=\tan^2x\cdot\sin^2x\).
Chọn phương án C.
\(\begin{aligned}
M&=\tan^2x-\sin^2x\\
&=\dfrac{\sin^2x}{\cos^2x}-\sin^2x\\
&=\dfrac{\sin^2x-\sin^2x\cdot\cos^2x}{\cos^2x}\\
&=\dfrac{\sin^2x\left(1-\cos^2x\right)}{\cos^2x}\\
&=\dfrac{\sin^2x\cdot\sin^2x}{\cos^2x}\\
&=\dfrac{\sin^2x}{\cos^2x}\cdot\sin^2x\\
&=\tan^2x\cdot\sin^2x.
\end{aligned}\)
