Ngân hàng bài tập
C
Tính giới hạn \(\lim\limits_{x\to-3^+}\dfrac{x^2+13x+30}{\sqrt{(x+3)(x^2+5)}}\).
| \(-2\) | |
| \(2\) | |
| \(0\) | |
| \(\dfrac{2}{\sqrt{15}}\) |
2 lời giải
Chọn phương án C.
Dùng máy tính cầm tay:
- Dùng chức năng r, với \(x=-2,999\)
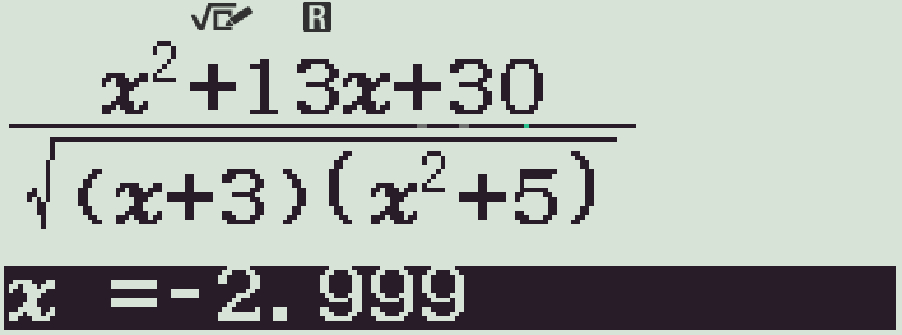
- Kết quả xấp xỉ bằng \(0\)
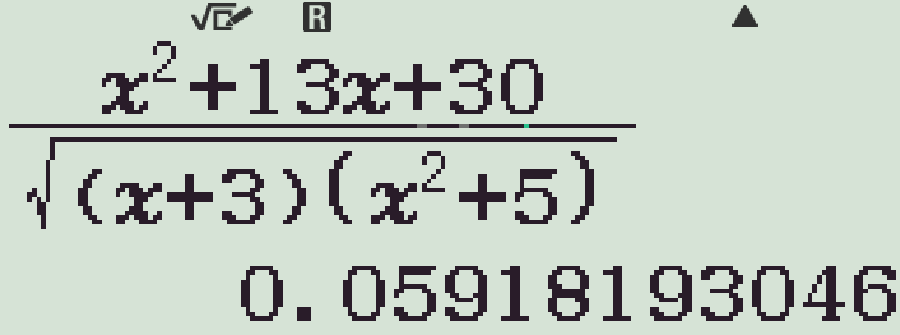
Chọn phương án C.
Khi \(x\to-3^+\) thì \(x>-3\) nên \(x+3>0\).
Do đó $$\begin{aligned}
\lim\limits_{x\to-3^+}\dfrac{x^2+13x+30}{\sqrt{(x+3)(x^2+5)}}&=\lim\limits_{x\to-3^+}\dfrac{(x+10)(x+3)}{\sqrt{x+3}\sqrt{x^2+5}}\\
&=\lim\limits_{x\to-3^+}\dfrac{(x+10)\sqrt{x+3}}{\sqrt{x^2+5}}\\
&=\dfrac{(-3+10)\sqrt{-3+3}}{\sqrt{(-3)^2+5}}\\
&=0.
\end{aligned}$$
