Ngân hàng bài tập
A
Tập nghiệm của bất phương trình \(\dfrac{1}{x-1}\geq\dfrac{1}{x+1}\) là
| \((-1;1)\) | |
| \((-\infty;-1)\cup(1;+\infty)\) | |
| \((-\infty;-1]\cup[1;+\infty)\) | |
| \((-\infty;-1)\) |
1 lời giải
Chọn phương án B.
\(\begin{aligned}
&\,\dfrac{1}{x-1}\geq\dfrac{1}{x+1}\\
\Leftrightarrow&\,\dfrac{1}{x-1}-\dfrac{1}{x+1}\geq0\\
\Leftrightarrow&\,\dfrac{(x+1)-(x-1)}{(x-1)(x+1)}\geq0\\
\Leftrightarrow&\,\dfrac{2}{(x-1)(x+1)}\geq0.
\end{aligned}\)
Xét dấu vế trái ta được: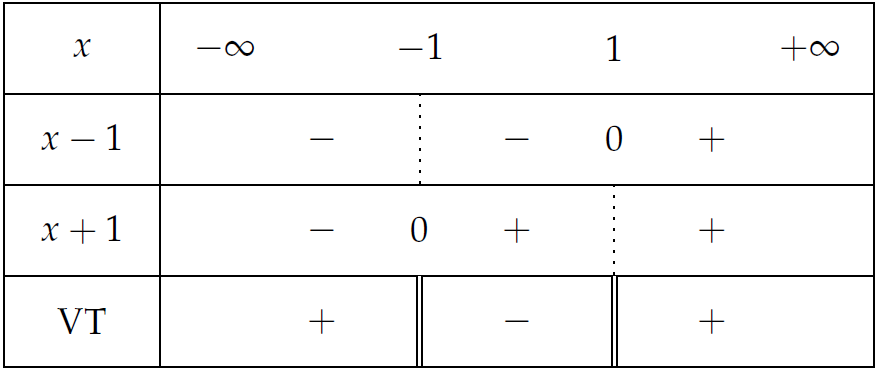
Vậy tập nghiệm của bất phương trình là \((-\infty;-1)\cup(1;+\infty)\).
