Ngân hàng bài tập
C
Giới hạn \(\lim\limits_{x\to3^-}\dfrac{x^2+2x-15}{|x-3|}\) bằng
| \(8\) | |
| \(-\infty\) | |
| \(-8\) | |
| Không tồn tại |
2 lời giải
Chọn phương án C.
Dùng chức năng r trên máy tính cầm tay, với \(x=2,999\) ta thu được kết quả cần tìm là \(-8\).
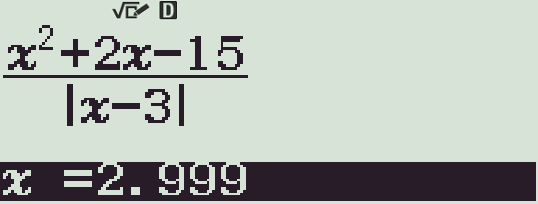

Chọn phương án C.
\(\begin{aligned}
\lim\limits_{x\to3^-}\dfrac{x^2+2x-15}{|x-3|}&=\lim\limits_{x\to3^-}\dfrac{(x-3)(x+5)}{-(x-3)}\\
&=\lim\limits_{x\to3^-}\dfrac{x+5}{-1}\\
&=\dfrac{3+5}{-1}=-8.
\end{aligned}\)
