Ngân hàng bài tập
A
Cho phương trình \(x^2+y^2-2x+2my+10=0\) (1). Có bao nhiêu giá trị \(m\) nguyên dương không vượt quá \(10\) để (1) là phương trình của đường tròn?
| Không có | |
| \(6\) | |
| \(7\) | |
| \(8\) |
1 lời giải
Chọn phương án C.
Ta có \(\begin{cases}
a=\dfrac{-2}{-2}=1\\
b=\dfrac{2m}{-2}=-m\\
c=10.
\end{cases}\)
Để \(\left(1\right)\) là phương trình của đường tròn thì $$\begin{eqnarray*}
&a^2+b^2-c&>0\\
\Leftrightarrow&1^2+(-m)^2-10&>0\\
\Leftrightarrow&m^2-9&>0.
\end{eqnarray*}$$
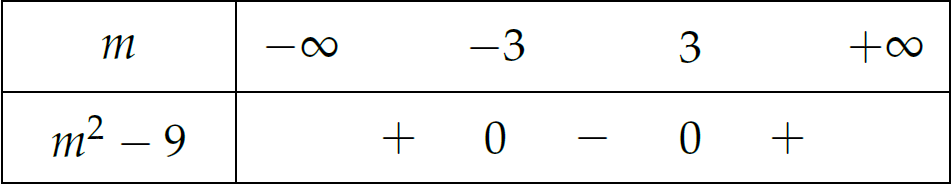
Suy ra \(m\in(-\infty;-3)\cup(3;+\infty)\).
Vì \(m\) nguyên dương và không vượt quá \(10\) nên \(m\in(3;10]\).
Vậy có \(7\) giá trị của \(m\) thỏa đề là $$\{4;5;6;7;8;9;10\}.$$
