Biết \(\displaystyle\int\limits_{\ln2}^{\ln5}(x+1)\mathrm{e}^x \mathrm{\,d}x=a\ln5+b\ln2\), với \(a,\,b\) là các số nguyên. Tính \(T=3a-2b\).
| \(T=19\) | |
| \(T=-4\) | |
| \(T=11\) | |
| \(T=-16\) |
Chọn phương án A.
Dùng máy tính cầm tay:
- Lưu tích phân \(\displaystyle\int\limits_{\ln2}^{\ln5}(x+1)\mathrm{e}^x\mathrm{\,d}x\) vào biến nhớ A
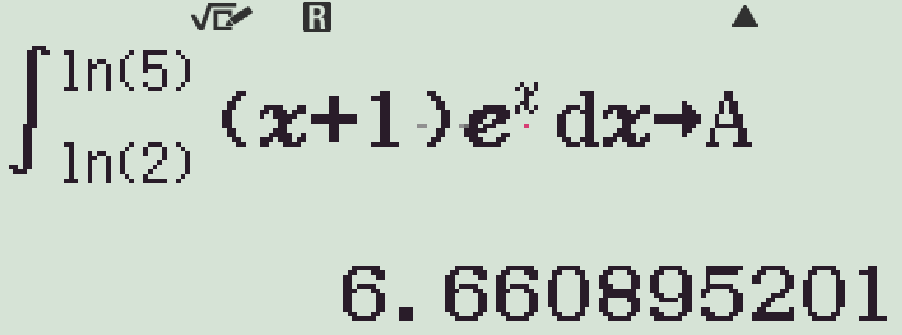
- Xem \(a\) là một biến số nguyên, ta được \(b=f(a)\) như sau:
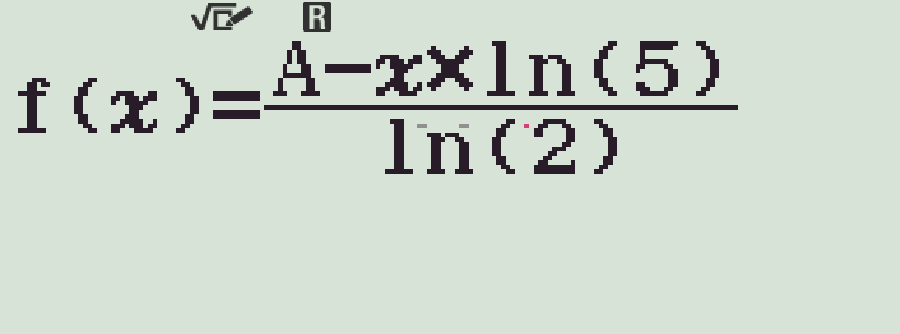
- Cho \(a\) biến thiên trên đoạn \([-10;10]\), bước nhảy bằng \(1\)
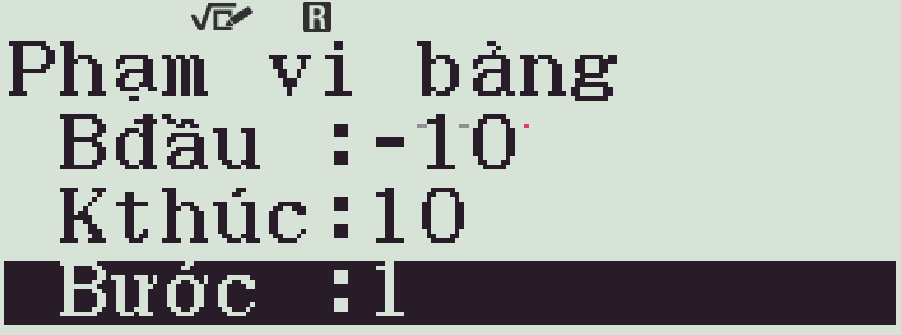
- Chọn giá trị \(f(x)\) nguyên đủ nhỏ
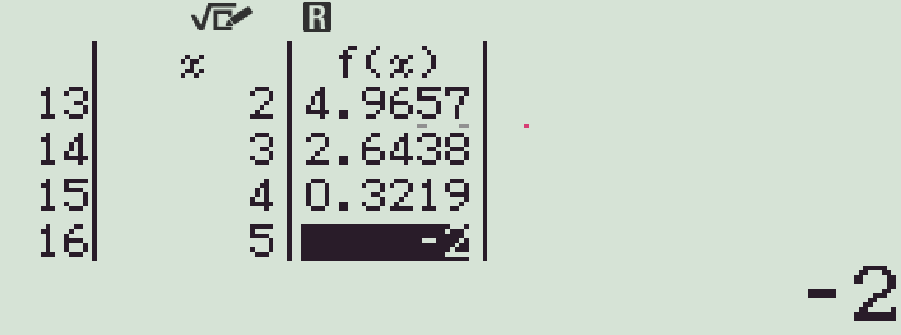
Vậy \(\begin{cases}a=5\\b=-2\end{cases}\). Do đó \(T=3a-2b=19\).
Chọn phương án A.
Đặt \(\begin{cases}
u=x+1\\\mathrm{\,d}v=\mathrm{e}^x\mathrm{\,d}x
\end{cases}\Rightarrow\begin{cases}
\mathrm{\,d}u=\mathrm{\,d}x\\v=\mathrm{e}^x.
\end{cases}\)
Khi đó: $$\begin{aligned}
\displaystyle\int\limits_{\ln2}^{\ln5}(x+1)\mathrm{e}^x \mathrm{\,d}x&=(x+1)\mathrm{e}^x\bigg|_{\ln2}^{\ln5} -\displaystyle\int\limits_{\ln2}^{\ln5}\mathrm{e}^x \mathrm{\,d}x\\
&=5\left(\ln5+1\right)-2\left(\ln2+1\right)-\mathrm{e}^x \bigg|_{\ln2}^{\ln{5}}\\
&=5\left(\ln5+1\right)-2\left(\ln2+1\right)-3\\
&=5\ln{5}-2\ln{2}.
\end{aligned}$$
Vậy \(\begin{cases}
a=5\\b=-2
\end{cases}\). Do đó \(T=3a-2b=19\).
