Ngân hàng bài tập
C
Cho \(a\) là số thực dương. Mệnh đề nào dưới đây đúng?
| \(|x|\geq a\Leftrightarrow-a\leq x\leq a\) | |
| \(|x|\leq a\Leftrightarrow x\leq a\) | |
| \(|x|>a\Leftrightarrow x>a\) | |
| \(|x|\geq a\Leftrightarrow\left[\begin{array}{l}x\geq a\\ x\leq-a\end{array}\right.\) |
1 lời giải
Chọn phương án D.
Vì \(a>0\) nên $$\begin{aligned}|x|\geq a\Leftrightarrow&\,x^2\geq a^2\\
\Leftrightarrow&\,x^2-a^2\geq0\\
\Leftrightarrow&\,(x-a)(x+a)\geq0.\end{aligned}$$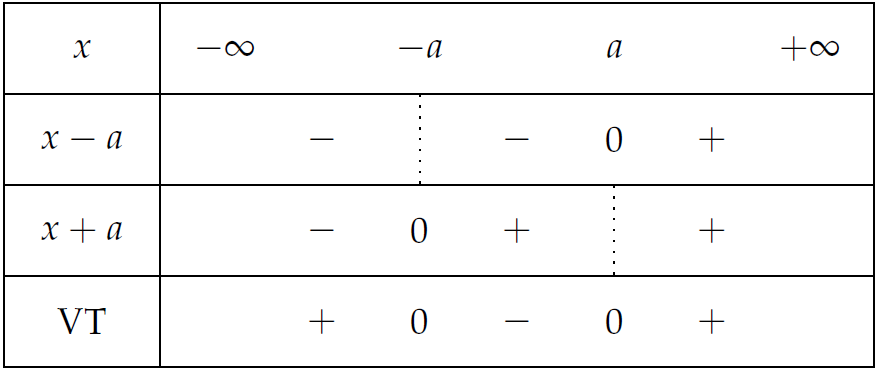
Do đó \(\left[\begin{array}{l}x\geq a\\ x\leq-a\end{array}\right.\)
