Ngân hàng bài tập
S
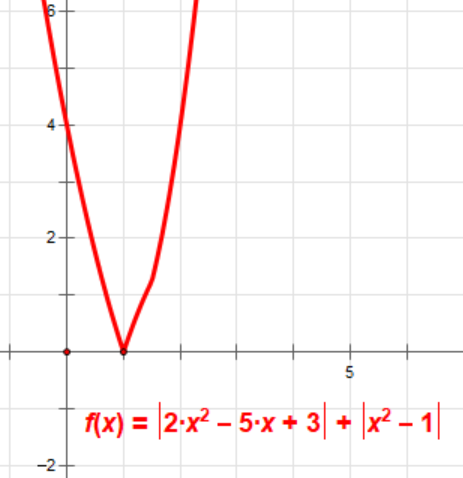
Tập nghiệm của bất phương trình \(\left|2x^2-5x+3\right|+\left|x^2-1\right|\leq0\) là
| \(\left[\dfrac{2}{3};4\right]\) | |
| \(\left[\dfrac{2}{3};4\right]\setminus\{1\}\) | |
| \(\varnothing\) | |
| \(\{1\}\) |
1 lời giải
Chọn phương án D.
Ta có \(\left|2x^2-5x+3\right|+\left|x^2-1\right|\geq0\), \(\forall x\in\Bbb{R}\).
\(\begin{aligned}
\text{Vậy }&\,\left|2x^2-5x+3\right|+\left|x^2-1\right|\leq0\\
\Leftrightarrow&\,\left|2x^2-5x+3\right|+\left|x^2-1\right|=0\\
\Leftrightarrow&\,\begin{cases}
\left|2x^2-5x+3\right|=0\\
\left|x^2-1\right|=0
\end{cases}\\
\Leftrightarrow&\,\begin{cases}
2x^2-5x+3=0\\
x^2-1=0
\end{cases}\\
\Leftrightarrow&\,\begin{cases}
\left[\begin{array}{l}x=1\\ x=\dfrac{3}{2}\end{array}\right.\\
\left[\begin{array}{l}x=1\\ x=-1\end{array}\right.
\end{cases}\\
\Leftrightarrow&\,x=1.
\end{aligned}\)