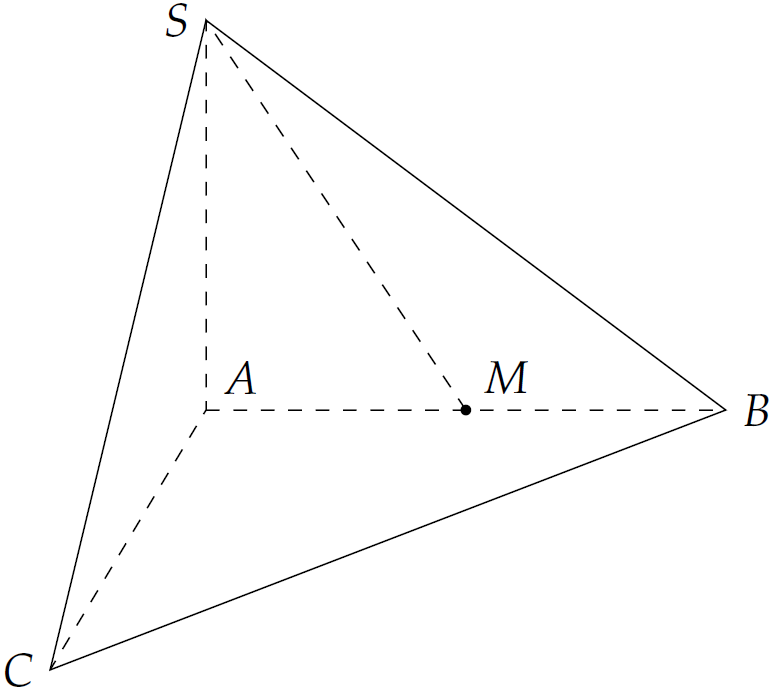
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(A\), \(AB=2a\), \(AC=4a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA=a\) (minh họa như hình vẽ). Gọi \(M\) là trung điểm của \(AB\). Khoảng cách giữa hai đường thẳng \(SM\) và \(BC\) bằng
| \(\dfrac{2a}{3}\) | |
| \(\dfrac{a\sqrt{6}}{3}\) | |
| \(\dfrac{a\sqrt{3}}{3}\) | |
| \(\dfrac{a}{2}\) |
Chọn phương án A.
Gọi \(N\) là trung điểm cạnh \(AC\), khi đó \(BC\parallel MN\).
Suy ra \(BC\parallel(SMN)\).
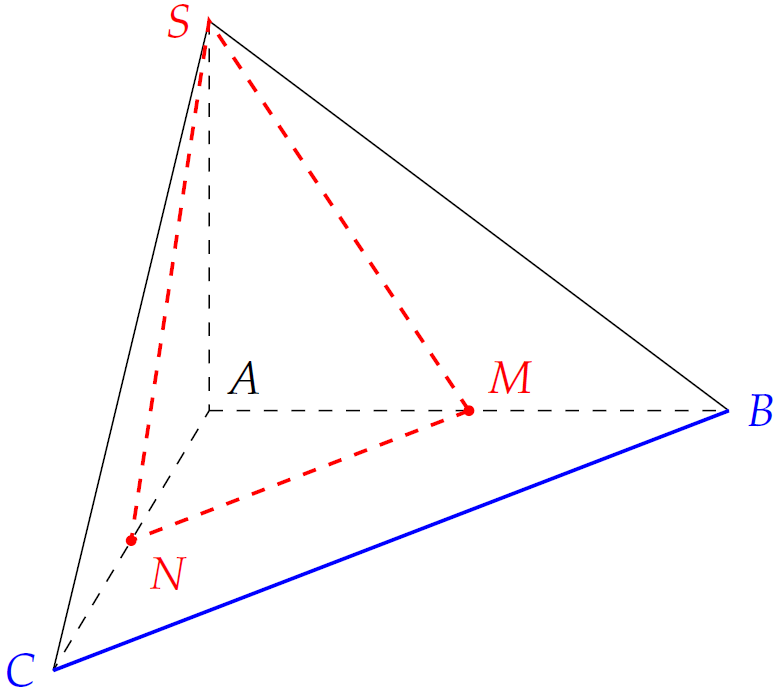
Vì \(AB,\,AC,\,AS\) đôi một vuông góc nên ta đặt hình chóp \(S.ABC\) vào hệ tọa độ \(Oxyz\) sao cho \(A\equiv O\), \(B\in Oy\), \(C\in Ox\), \(S\in Oz\).
Xem \(a=1\) (đơn vị) ta có \(A(0;0;0)\), \(B(0;2;0)\), \(C(4;0;0)\), \(S(0;0;1)\), \(M(0;1;0)\), \(N(2;0;0)\).
Ta có phương trình đoạn chắn $$(SMN)\colon\dfrac{x}{2}+\dfrac{y}{1}+\dfrac{z}{1}=1\Leftrightarrow x+2y+2z-2=0.$$
Khi đó \(\mathrm{d}\left(C,(SMN)\right)=\dfrac{\left| 4+0+0-2 \right|}{\sqrt{1^2+2^2+2^2}}=\dfrac{2}{3}\).
Vậy \(\mathrm{d}\left(SM,BC\right)=\dfrac{2a}{3}\).
