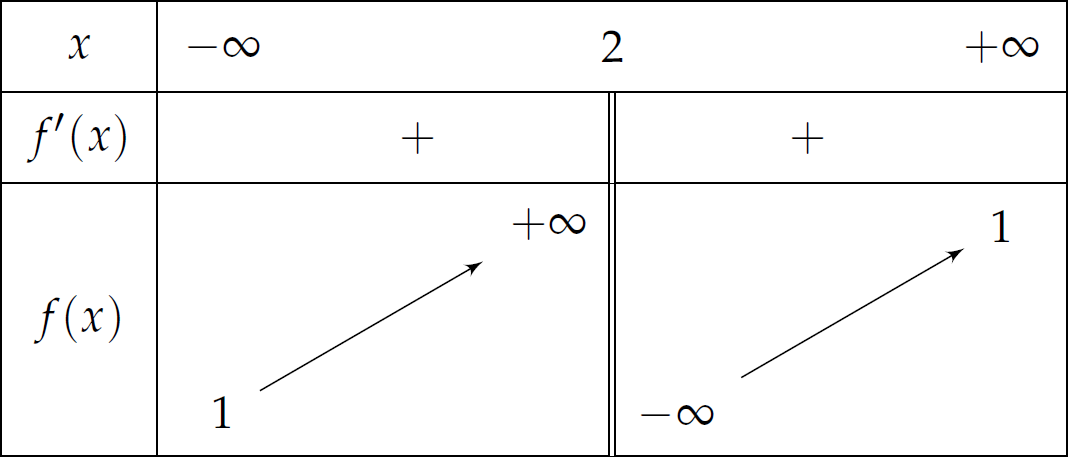
Cho hàm số \(f\left(x\right)=\dfrac{ax+1}{bx+c}\) \(\left(a,b,c\in\mathbb{R}\right)\) có bảng biến thiên như sau:
Trong các số \(a,\,b\) và \(c\) có bao nhiêu số dương?
| \(2\) | |
| \(3\) | |
| \(1\) | |
| \(0\) |
Chọn phương án C.
- Dựa vào bảng biến thiên ta thấy $$f(0)=\dfrac{1}{c}>1>0\Rightarrow c>0$$
- Tiệm cận đứng: $x=-\dfrac{c}{b}=2>0\Rightarrow\dfrac{c}{b}<0\Rightarrow b<0$
- Tiệm cận ngang: $y=\dfrac{a}{b}=1\Rightarrow a=b<0$
Vậy có $1$ số dương là $c$.
Ý tưởng của bạn Võ Hoàng Luân.
Chọn phương án C.
Ta có \(\lim\limits_{x\to+\infty}\dfrac{ax+1}{bx+c}=\lim\limits_{x\to+\infty}\dfrac{a+\dfrac{1}{x}}{b+\dfrac{c}{x}}=\dfrac{a}{b}\).
Theo giả thiết, ta có \(\dfrac{a}{b}=1\Rightarrow a=b\) (1).
Hàm số không xác định tại \(x=2\) nên suy ra $$2b+c=0\Rightarrow b=-\dfrac{c}{2}\;(2)$$
Vì hàm số đồng biến trên các khoảng xác định nên $$f'\left(x\right)=\dfrac{ac-b}{\left(bx+c\right)^2}>0,\,\forall x\neq2\;(3)$$
Nếu \(a=b>0\) thì từ (2) suy ra \(c<0\).
Thay vào (3), ta thấy vô lý nên trường hợp này không xảy ra.
Suy ra, chỉ có thể xảy ra khả năng \(a=b<0\) và \(c>0\).

