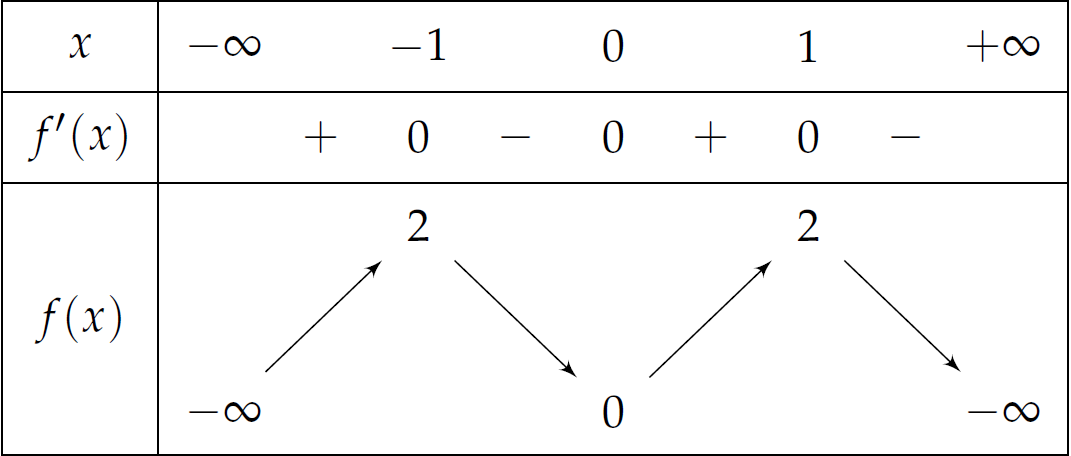
Cho hàm số \(f\left(x\right)\) có bảng biến thiên như sau:
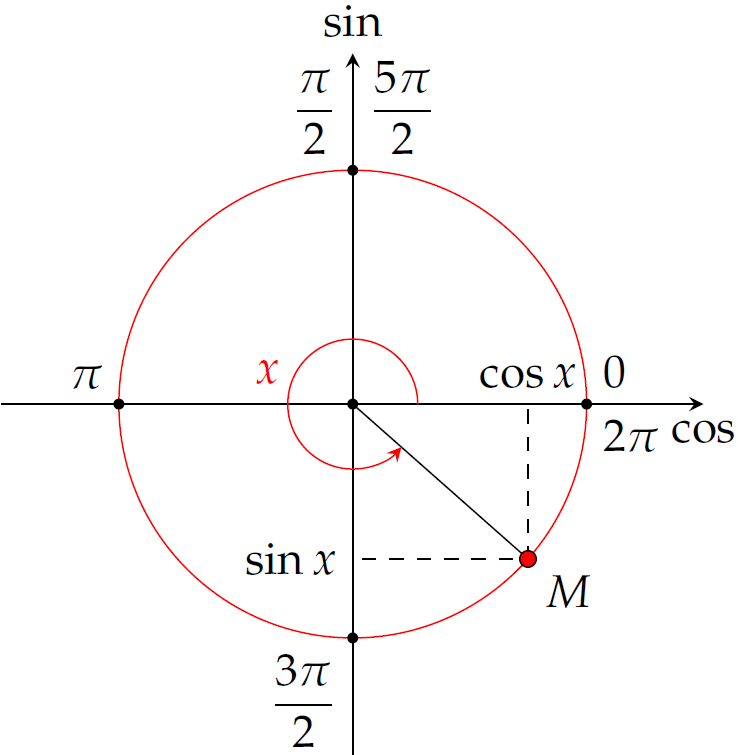
Số nghiệm thuộc đoạn \(\left[0;\dfrac{5\pi}{2}\right]\) của phương trình \(f\left(\sin x\right)=1\) là
| \(7\) | |
| \(4\) | |
| \(5\) | |
| \(6\) |
Chọn phương án C.
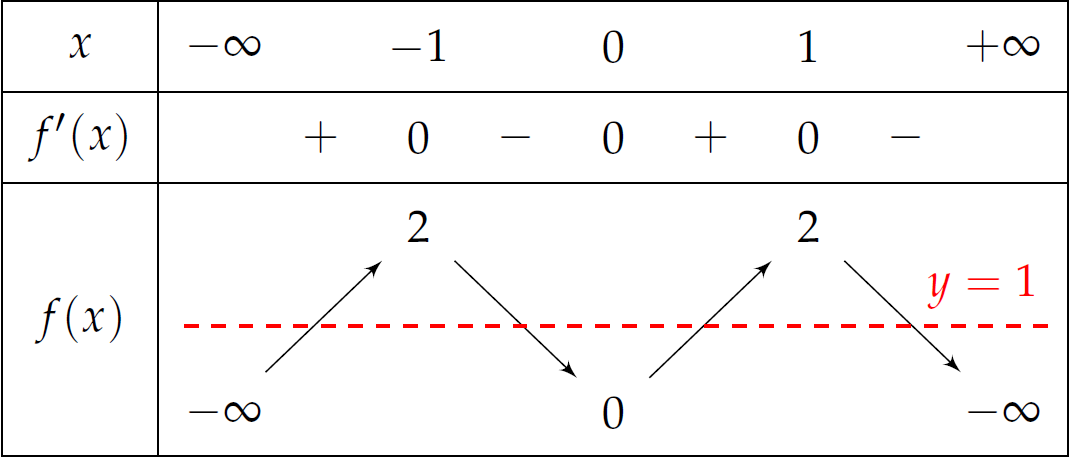
Dựa vào bảng biến thiên, ta có $$f\left(x\right)=1\Leftrightarrow\left[\begin{array}{ll}
x=a &\in\left(-\infty;-1\right) \\
x=b &\in\left(-1;0\right) \\
x=c &\in\left(0;1\right) \\
x=d &\in\left(1;+\infty\right).\end{array}\right.$$
Như vậy ta có $$f\left(\sin x\right)=1\Leftrightarrow\left[\begin{array}{ll}
\sin x=a\in\left(-\infty;-1\right) &\left(1\right) \\
\sin x=b\in\left(-1;0\right) &\left(2\right) \\
\sin x=c\in\left(0;1\right) &\left(3\right) \\
\sin x=d\in\left(1;+\infty\right) &\left(4\right).
\end{array}\right.$$
Vì \(\sin x\in\left[0;1\right],\;\forall x\) nên (1) và (4) vô nghiệm.
- Từ (2) suy ra \(\sin x<0\).
Vậy \(x\in\left(\pi;\dfrac{3\pi}{2}\right)\) hoặc \(x\in\left(\dfrac{3\pi}{2};2\pi\right)\). - Từ (3) suy ra \(\sin x>0\).
Vậy \(x\in\left(0;\dfrac{\pi}{2}\right)\), \(x\in\left(\dfrac{\pi}{2};\pi\right)\) hoặc \(x\in\left(2\pi;\dfrac{5\pi}{2}\right)\).