Cho hình hộp \(ABCD.A'B'C'D'\) có chiều cao bằng \(8\) và diện tích đáy bằng \(9\). Gọi \(M,\,N,\,P\) và \(Q\) lần lượt là tâm của các mặt bên \(ABB'A'\), \(BCC'B'\), \(CDD'C'\) và \(DAA'D'\). Thể tích của khối đa diện lồi có các đỉnh là các điểm \(A,\,B,\,C,\,D\), \(M,\,N,\,P\) và \(Q\) bằng
| \(27\) | |
| \(30\) | |
| \(18\) | |
| \(36\) |
Chọn phương án B.
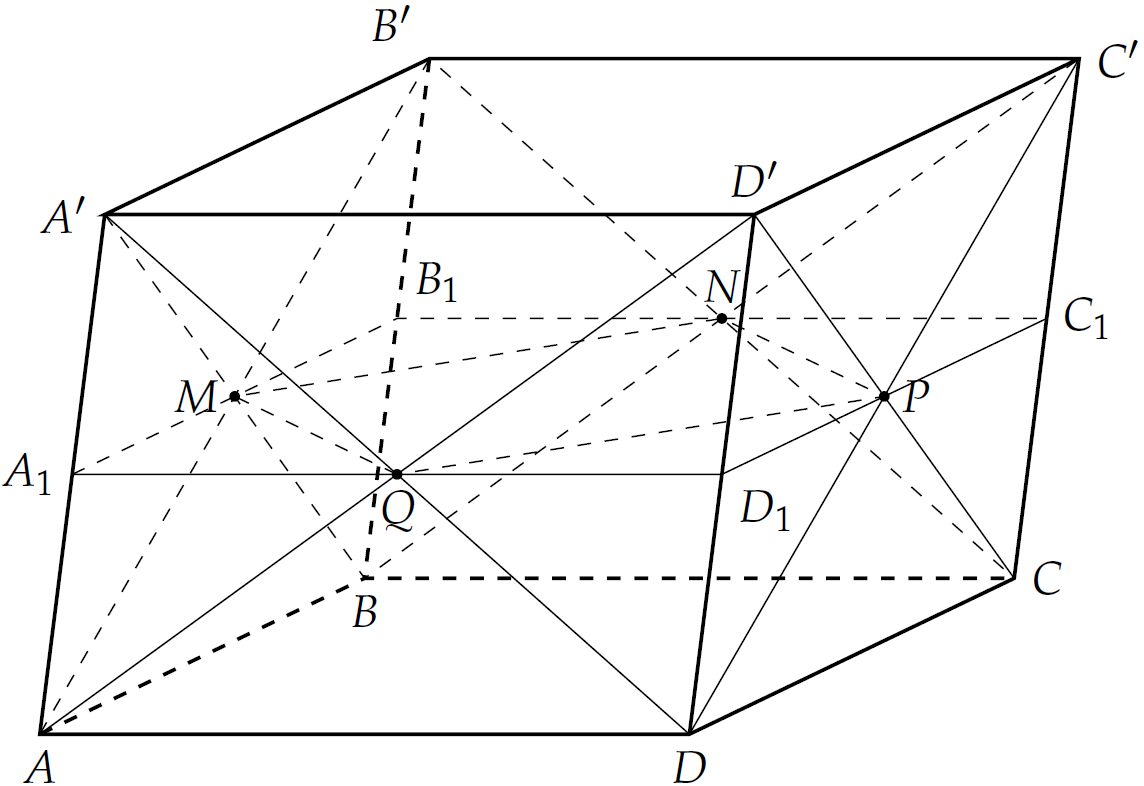
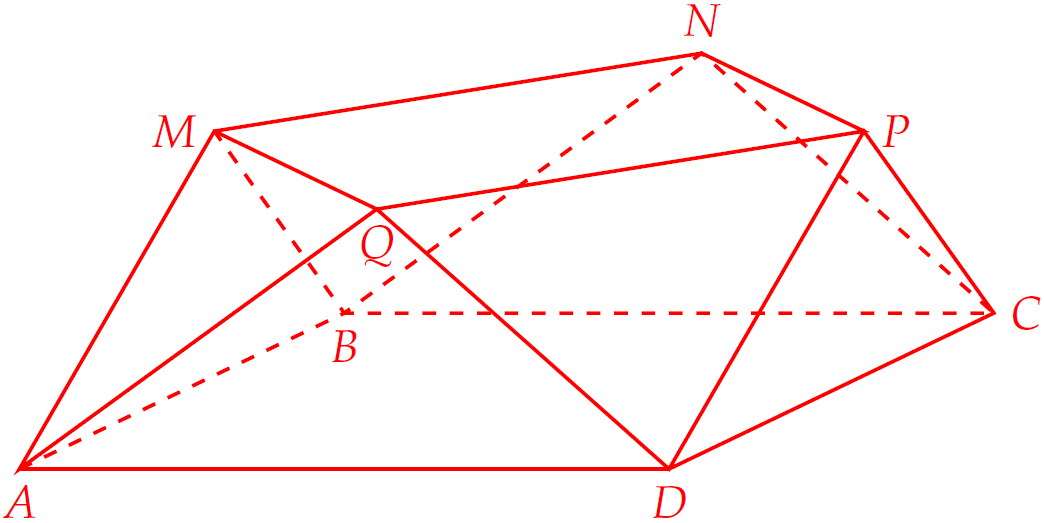
Ta có bốn điểm \(M,\,N,\,P,\,Q\) đồng phẳng.
Gọi \(A_1,\,B_1,\,C_1,\,D_1\) lần lượt là giao điểm của \(\left(MNPQ\right)\) và các cạnh \(AA',\,BB',\,CC',\,DD'\).
Khi đó \(A_1,\,B_1,\,C_1,\,D_1\) lần lượt là trung điểm của \(AA',\,BB',\,CC',\,DD'\).
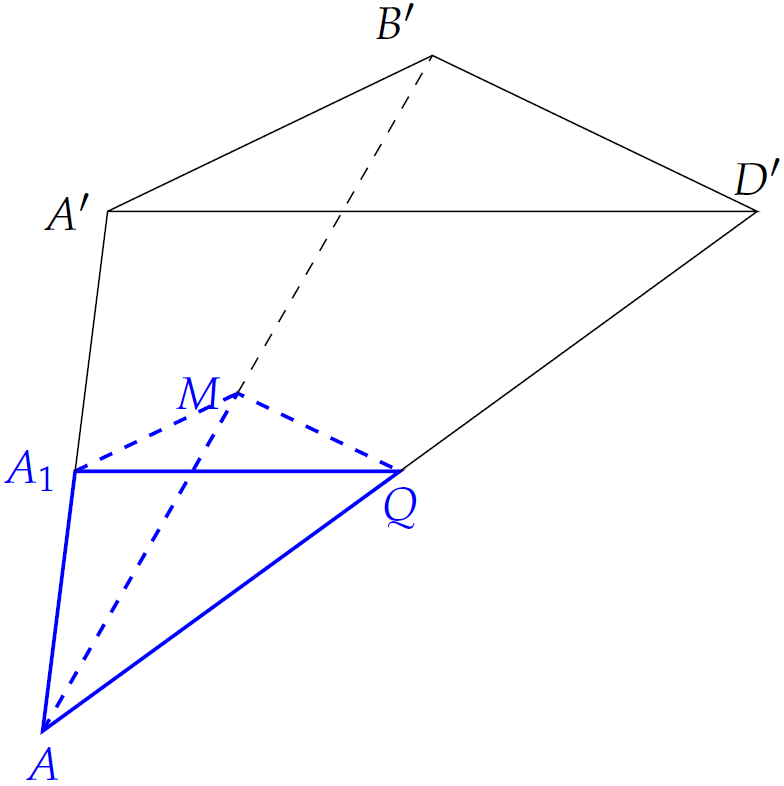
\dfrac{V_{A.A_1MQ}}{V_{A.A'B'D'}}&=\dfrac{AA_1}{AA'}\cdot\dfrac{AM}{AB'}\cdot\dfrac{AQ}{AD'}\\
&=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot\dfrac{1}{2}=\dfrac{1}{8}.
\end{aligned}$$Suy ra $$\begin{aligned}
V_{A.A_1MQ}&=\dfrac{1}{8}\cdot V_{A.A'B'D'}\\
&=\dfrac{1}{8}\cdot \dfrac{1}{3}S_{A'B'D'}\cdot h\\
&=\dfrac{1}{24}\cdot\dfrac{1}{2}S_{A'B'C'D'}\cdot8\\
&=\dfrac{1}{6}\cdot9=\dfrac{3}{2}.
\end{aligned}$$
Tương tự, ta cũng tính được $$V_{B.B_1MN}=V_{C.C_1NP}=V_{D.D_1PQ}=\dfrac{3}{2}.$$
Vậy thể tích của khối đa diện lồi cần tìm là
$$\begin{aligned}
V&=V_{ABCD.A_1B_1C_1D_1}-\left(V_{A.A_1MQ}+V_{B.B_1MN}+V_{C.C_1NP}+V_{D.D_1PQ}\right)\\
&=36-4\cdot\dfrac{3}{2}=30.
\end{aligned}$$
