Ngân hàng bài tập
C
Tìm giá trị nhỏ nhất \(m\) của hàm số $$y=\dfrac{1}{\cos x+1}.$$
| \(m=\dfrac{1}{2}\) | |
| \(m=\dfrac{1}{\sqrt{2}}\) | |
| \(m=1\) | |
| \(m=\sqrt{2}\) |
2 lời giải
Chọn phương án A.
Dùng chức năng TABLE của máy tính cầm tay
- Đưa máy tính về đơn vị độ (DEG) cho dễ chọn bước nhảy
- Chọn chế độ một hàm \(f(x)\) trong TABLE
- Nhập hàm số \(f(x)=\dfrac{1}{\cos x+1}\)

- Chọn bước nhảy thích hợp với cấu hình của máy
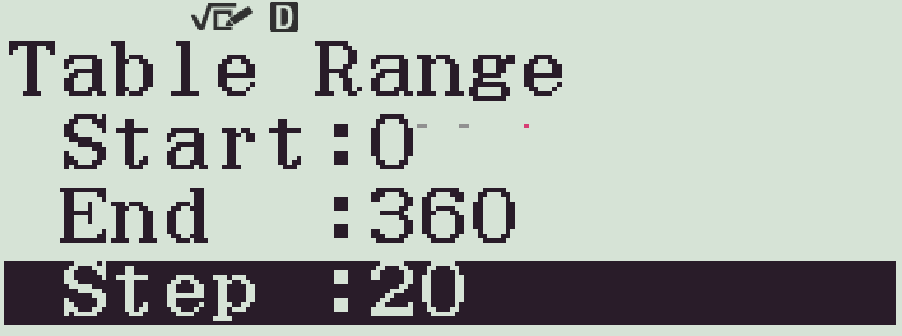
- Quan sát, tìm GTLN và GTNN

Theo đó \(m\approx\dfrac{1}{2}\).
Chọn phương án A.
Với mọi \(x\in\mathbb{R}\) ta có $$\cos x\leq1\Leftrightarrow\cos x+1\leq2\Leftrightarrow\dfrac{1}{\cos x+1}\geq\dfrac{1}{2}.$$
Vậy \(m=\dfrac{1}{2}\).
