Ngân hàng bài tập
B
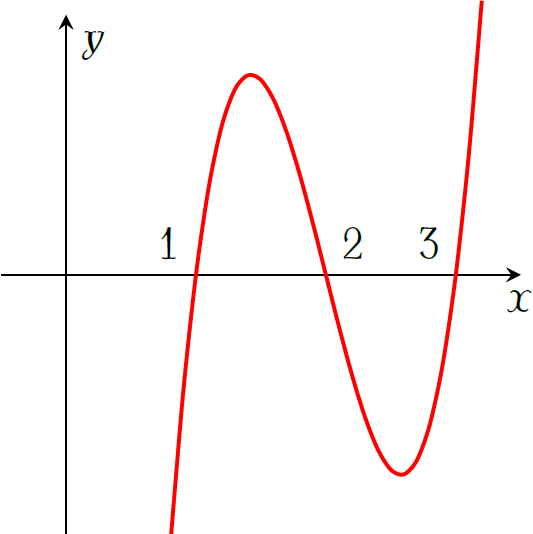
Cho hàm số \(y=f(x)\) liên tục trên \(\mathbb{R}\). Hàm số \(y=f'(x)\) có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
| Đồ thị hàm số \(y=f(x)\) có \(2\) điểm cực trị | |
| Đồ thị hàm số \(y=f(x)\) có \(3\) điểm cực trị | |
| Đồ thị hàm số \(y=f(x)\) có \(1\) điểm cực trị | |
| Đồ thị hàm số \(y=f(x)\) có \(4\) điểm cực trị |
1 lời giải
Chọn phương án B.
Theo hình vẽ ta thấy \(f'(x)=0\Leftrightarrow\left[\begin{array}{l}x=1\\ x=2\\ x=3\end{array}\right.\)
Mặt khác, vì \(f'(x)\) đổi dấu khi đi qua ba điểm này nên suy ra hàm số \(y=f(x)\) có \(3\) điểm cực trị.
