Cho tam giác \(ABC\) đều cạnh \(a\), trọng tâm \(G\). Tích vô hướng \(\overrightarrow{BC}\cdot\overrightarrow{CG}\) bằng
| \(\dfrac{a^2}{\sqrt{2}}\) | |
| \(-\dfrac{a^2}{\sqrt{2}}\) | |
| \(\dfrac{a^2}{2}\) | |
| \(-\dfrac{a^2}{2}\) |
Chọn phương án D.
Dựng hệ trục tọa độ \(Oxy\) sao cho trung điểm \(M\) của cạnh \(BC\) trùng với gốc tọa độ \(O\), cạnh \(BC\) trùng với trục hoành, đường cao \(AM\) trùng với trục tung.
Khi đó \(B\left(-\dfrac{a}{2};0\right)\), \(C\left(\dfrac{a}{2};0\right)\), \(A\left(0;\dfrac{\sqrt{3}}{2}\right)\) và \(G\left(0;\dfrac{a\sqrt{3}}{3}\right)\).
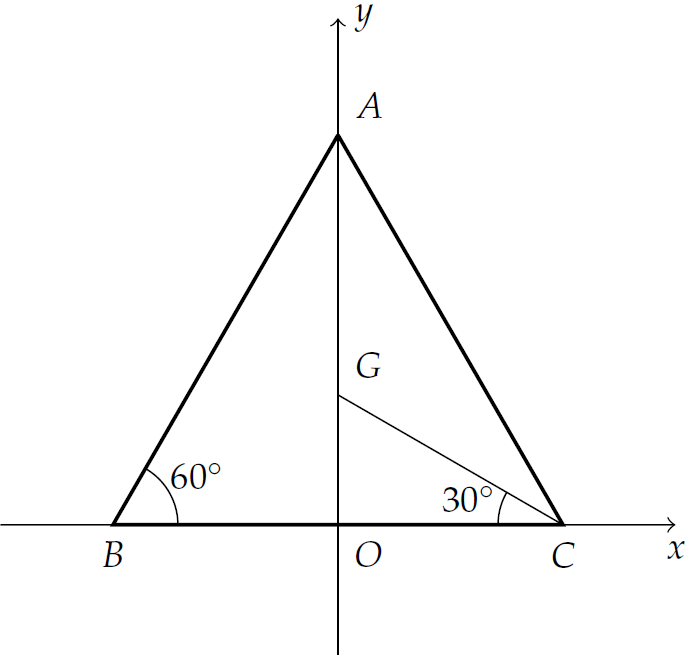
Ta có \(\overrightarrow{BC}=\left(a;0\right)\), \(\overrightarrow{CG}=\left(-\dfrac{a}{2};\dfrac{a\sqrt{3}}{3}\right)\).
Suy ra $$\overrightarrow{BC}\cdot\overrightarrow{CG}=a\cdot\left(-\dfrac{a}{2}\right)+0\cdot\dfrac{a\sqrt{3}}{3}=-\dfrac{a^2}{2}.$$
Chọn phương án D.
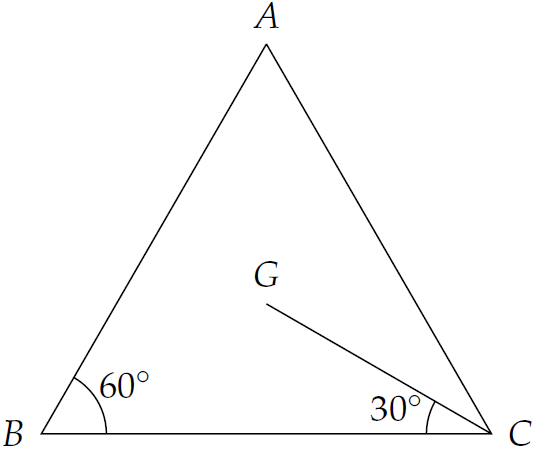
\(\begin{aligned}
\overrightarrow{BC}\cdot\overrightarrow{CG}&=-\overrightarrow{CB}\cdot\overrightarrow{CG}\\
&=-CB\cdot CG\cdot\cos\widehat{BCG}\\
&=-a\cdot\left(\dfrac{2}{3}\cdot\dfrac{a\sqrt{3}}{2}\right)\cos30^\circ\\
&=-\dfrac{a^2}{2}.
\end{aligned}\)
