Ngân hàng bài tập
B
Giải phương trình \(\cot(3x-1)=-\sqrt{3}\).
| \(x=\dfrac{1}{3}+\dfrac{5\pi}{18}+k\dfrac{\pi}{3},\,k\in\mathbb{Z}\) | |
| \(x=\dfrac{1}{3}+\dfrac{\pi}{18}+k\dfrac{\pi}{3},\,k\in\mathbb{Z}\) | |
| \(x=\dfrac{5\pi}{18}+k\dfrac{\pi}{3},\,k\in\mathbb{Z}\) | |
| \(x=\dfrac{1}{3}-\dfrac{\pi}{6}+k\pi,\,k\in\mathbb{Z}\) |
2 lời giải
Chọn phương án A.
Dùng chức năng r trên máy tính cầm tay.
- Chỉnh đơn vị góc về RAD và nhập phương trình vào máy
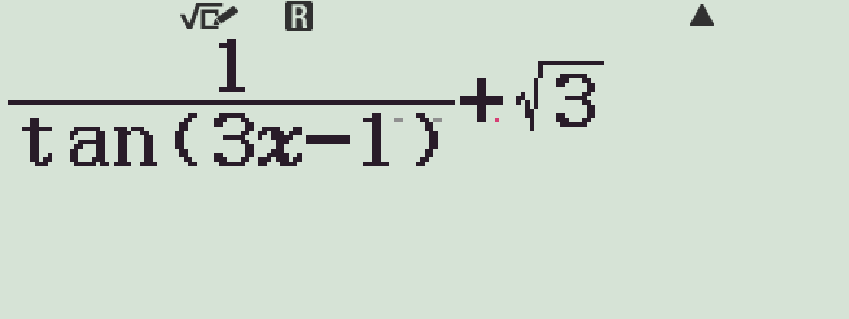
- Dùng chức năng r kiểm tra từng phương án, với \(k=1\)
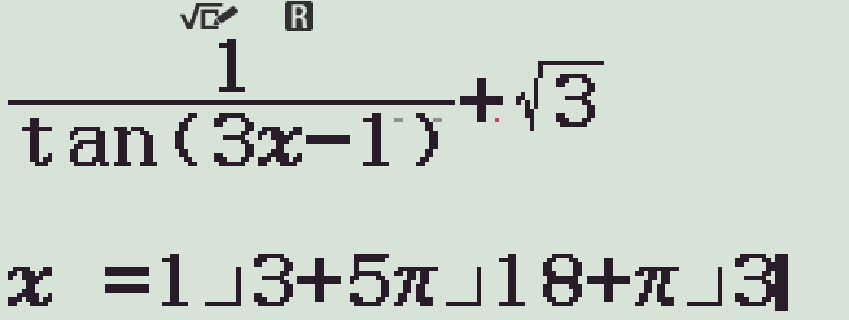
- Phương án nào cho kết quả bằng \(0\) là phương án cần tìm
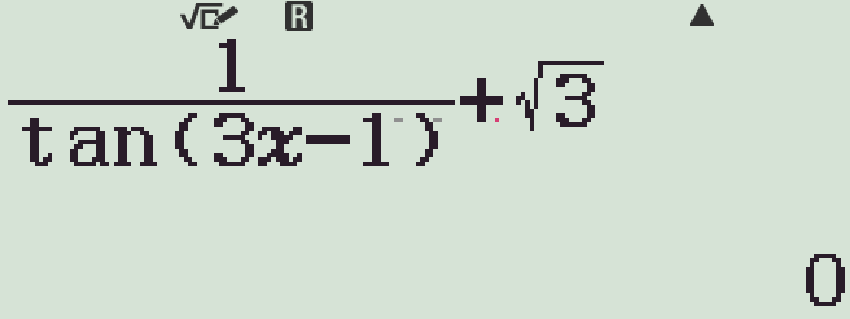
Chọn phương án A.
\(\begin{aligned}
\cot(3x-1)=-\sqrt{3}\Leftrightarrow&3x-1=\dfrac{5\pi}{6}+k\pi\\
\Leftrightarrow&3x=1+\dfrac{5\pi}{6}+k\pi\\
\Leftrightarrow&x=\dfrac{1}{3}+\dfrac{5\pi}{18}+k\dfrac{\pi}{3},\,k\in\mathbb{Z}.
\end{aligned}\)
