Ngân hàng bài tập
A
Cho tam giác \(ABC\) vuông tại \(A\), có \(\widehat{B}=60^\circ\) và \(AB=a\). Kết quả nào sau đây là sai?
| \(\overrightarrow{AC}\cdot\overrightarrow{CB}=-3a\sqrt{2}\) | |
| \(\overrightarrow{AB}\cdot\overrightarrow{BC}=-a^2\) | |
| \(\overrightarrow{AB}\cdot\overrightarrow{AC}=0\) | |
| \(\overrightarrow{CA}\cdot\overrightarrow{CB}=3a^2\) |
1 lời giải
Chọn phương án A.
Vì \(\triangle ABC\) vuông tại \(A\) nên \(\tan\widehat{B}=\dfrac{AC}{AB}\) \(\Rightarrow AC=AB\cdot\tan\widehat{B}=a\sqrt{3}\)và \(BC=\sqrt{AB^2+AC^2}=\sqrt{a^2+\left(a\sqrt{3}\right)^2}=2a\).
Do đó
- \(\overrightarrow{CA}\cdot\overrightarrow{CB}=CA\cdot CB\cdot\cos\widehat{BCA}\) \(=a\sqrt{3}\cdot2a\cos30^\circ=3a^2\)
- \(AB\bot AC\Rightarrow\overrightarrow{AB}\cdot\overrightarrow{AC}=0\)
- Dựng vectơ \(\overrightarrow{BD}=\overrightarrow{AB}\), khi đó \(\left(\overrightarrow{AB},\overrightarrow{BC}\right)=\left(\overrightarrow{BD},\overrightarrow{BC}\right)=\widehat{DBC}=120^\circ.\)
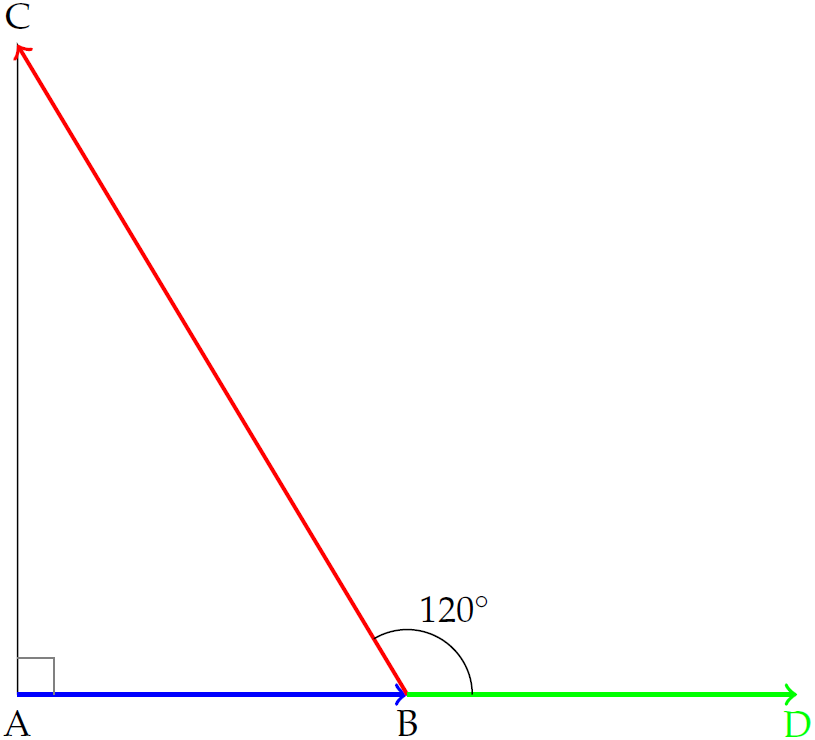
\(\begin{aligned}\overrightarrow{AB}\cdot\overrightarrow{BC}&=AB\cdot BC\cdot\cos\widehat{DBC}\\ &=a\cdot2a\cdot\cos120^\circ\\ &=-a^2.\end{aligned}\)
