Ngân hàng bài tập
B
Giá trị nhỏ nhất của hàm số \(y=x^2+2x+5\) trên nửa khoảng \([-4;+\infty)\) là
| \(13\) | |
| \(-17\) | |
| \(4\) | |
| \(-9\) |
1 lời giải
Chọn phương án C.
Ta có \(y'=2x+2\).
Cho \(y'=0\Leftrightarrow x=-1\).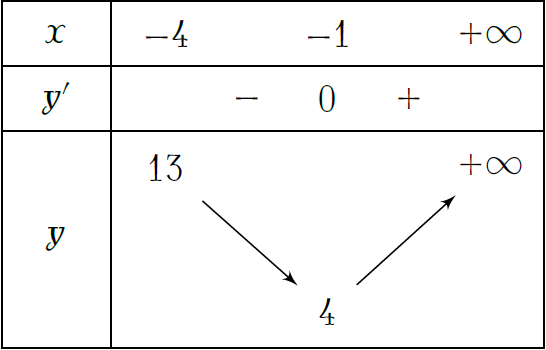
Vậy \(\min\limits_{[-4;+\infty)}y=4\).
