Một xưởng sản xuất cần làm \(100\) chiếc hộp inox bằng nhau, hình dạng là hình hộp chữ nhật có đáy là hình vuông (không có nắp), với thể tích là \(108\) dm\(^3\)/hộp. Giá của inox là \(47.000\) đồng/dm\(^2\). Hãy tính toán sao cho tổng chi phí sản xuất \(100\) chiếc hộp là ít nhất, và số tiền tối thiểu đó là bao nhiêu (nếu chỉ tính số inox vừa đủ để sản xuất \(100\) chiếc hộp, không có phần dư thừa, cắt bỏ)?
| \(1.692.000.000\) đồng | |
| \(507.666.000\) đồng | |
| \(1.015.200.000\) đồng | |
| \(235.800.000\) đồng |
Chọn phương án B.
Gọi \(x\) (dm) là độ dài cạnh đáy của hộp, \(h\) là chiều cao (\(x,\,h>0\)).
\(\Rightarrow h=\dfrac{108}{x^2}\) (dm).
Lượng inox để sản xuất mỗi chiếc hộp là $$S=S_{\text{đáy}}+S_{\text{xq}}=x^2+4x\cdot h=x^2+\dfrac{432}{x}\;(\text{dm}^2)$$
Vậy chi phí sản xuất \(100\) chiếc hộp là $$T=47.000\cdot100\cdot S=4.700.000\left(x^2+\dfrac{432}{x}\right)$$
Xét hàm số \(f(x)=x^2+\dfrac{432}{x}\).
Ta có \(f'(x)=2x-\dfrac{432}{x^2}=\dfrac{2x^3-432}{x^2}\).
Cho \(f'(x)=0\Leftrightarrow2x^3-432=0\Leftrightarrow x=6\).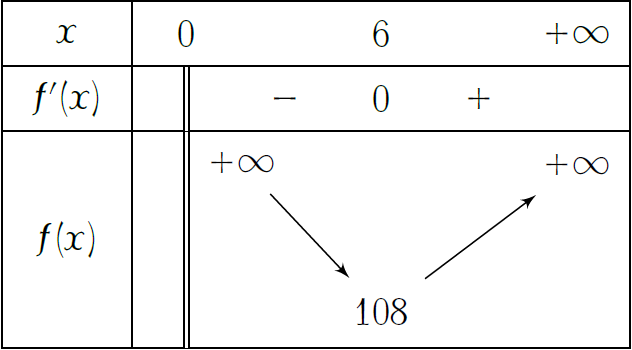
Theo đó, chi phí tối thiểu để sản xuất \(100\) chiếc hộp inox theo yêu cầu đề bài là $$T_{\min}=4.700.000\cdot108=507.600.000\text{ đồng.}$$
