Ngân hàng bài tập
C
Giải phương trình \(\sqrt{2x^2-8x+4}=x-2\) ta được
| \(x=4\) | |
| \(\left[\begin{array}{l}x=0\\ x=4\end{array}\right.\) | |
| \(x=4+2\sqrt{2}\) | |
| \(x=6\) |
2 lời giải
Chọn phương án A.
Chúng ta có thể dùng chức năng r trên máy tính cầm tay để kiểm tra xem giá trị nào là nghiệm. Giá trị nào cho kết quả bằng \(0\) chính là nghiệm.
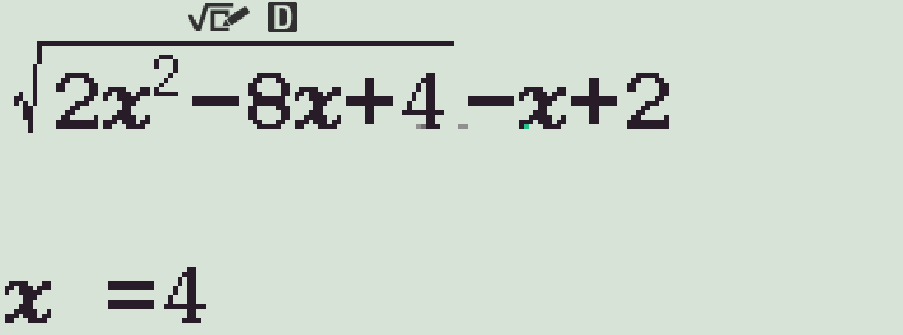
Chọn phương án A.
\(\begin{align*}&\,\sqrt{2x^2-8x+4}=x-2\\
\Leftrightarrow&\,\begin{cases}x-2\geq0\\ 2x^2-8x+4=(x-2)^2\end{cases}\\
\Leftrightarrow&\,\begin{cases}x\geq2\\ x^2-4x=0\end{cases}\\
\Leftrightarrow&\,\begin{cases}x\geq2\\ \left[\begin{array}{ll}x=0 &\text{(loại)}\\ x=4 &\text{(nhận)}\end{array}\right.\end{cases}
\end{align*}\)
Vậy phương trình có nghiệm duy nhất \(x=4\).
