Ngân hàng bài tập
B
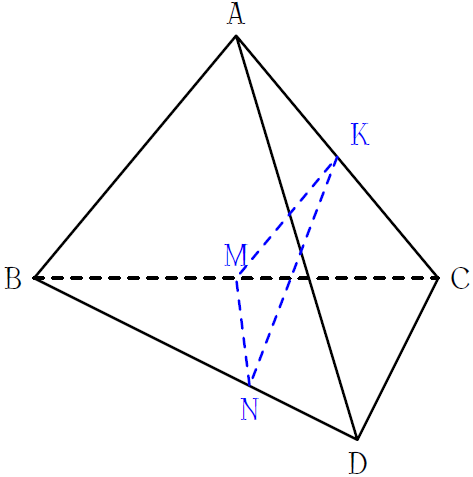
Cho tứ diện \(ABCD\). Gọi \(M,\,K\) lần lượt là trung điểm của \(BC\) và \(AC\), \(N\) là điểm trên cạnh \(BD\) sao cho \(BN=2ND\). Giao điểm của \(MN\) và \((ACD)\) là
| Giao điểm của \(MN\) với \(AD\) | |
| Giao điểm của \(MN\) với \(KD\) | |
| Giao điểm của \(MN\) với \(CD\) | |
| Không có |
1 lời giải
Chọn phương án C.
Trong mặt phẳng \((BCD)\), hai đường thẳng \(MN\) và \(CD\) không song song.
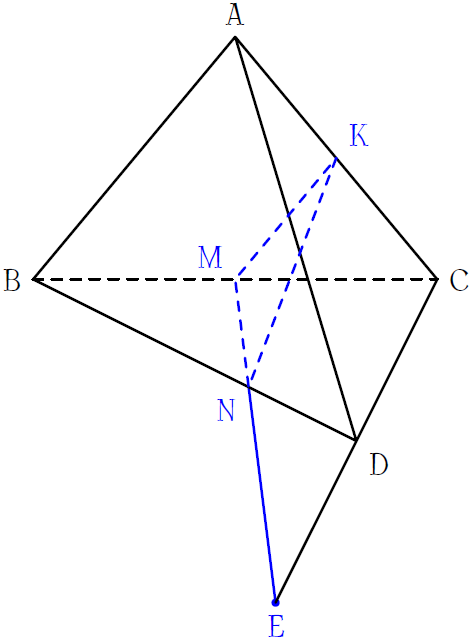
Gọi \(E=MN\cap CD\).
Khi đó \(\begin{cases}
E\in MN\\
E\in CD\Rightarrow E\in(ACD)
\end{cases}\)
Vậy \(E\) là giao điểm cần tìm.
