Ngân hàng bài tập
A
Cho hình chóp \(S.ABCD\) đáy là hình chữ nhật \(AD=2a\), \(AB=a\) (\(a>0\)), có \(\left(SAB\right)\) và \(\left(SAD\right)\) vuông góc đáy và góc \(SC\) và đáy bằng \(30^\circ\). Thể tích khối chóp là
| \(\dfrac{2a^3}{3}\) | |
| \(\dfrac{2a^3\sqrt{15}}{9}\) | |
| \(\dfrac{a^3\sqrt{3}}{3}\) | |
| \(\dfrac{a^3\sqrt{3}}{6}\) |
1 lời giải
Chọn phương án B.
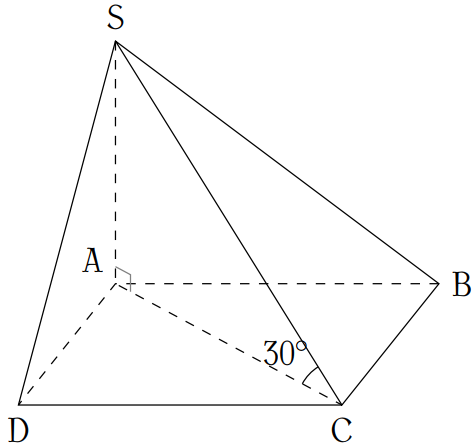
Diện tích đáy $$S_{ABCD}=AD\cdot AB=2a\cdot a=2a^2$$Vì \(\begin{cases}
(SAB)\bot(ABCD)\\
(SAD)\bot(ABCD)\\
(SAB)\cap(SAD)=SA
\end{cases}\) nên \(SA\bot(ABCD)\).
Xét tam giác vuông \(SAC\) ta có $$\tan\widehat{SCA}=\dfrac{SA}{AC}$$Suy ra $$\begin{aligned}
SA&=AC\cdot\tan\widehat{SCA}=\sqrt{AB^2+BC^2}\cdot\tan30^\circ\\
&=\sqrt{a^2+(2a)^2}\cdot\dfrac{\sqrt{3}}{3}=\dfrac{a\sqrt{15}}{3}
\end{aligned}$$
SA&=AC\cdot\tan\widehat{SCA}=\sqrt{AB^2+BC^2}\cdot\tan30^\circ\\
&=\sqrt{a^2+(2a)^2}\cdot\dfrac{\sqrt{3}}{3}=\dfrac{a\sqrt{15}}{3}
\end{aligned}$$
Khi đó $$\begin{aligned}V_{S.ABCD}&=\dfrac{1}{3}S_{ABCD}\cdot SA\\ &=\dfrac{1}{3}\cdot2a^2\cdot\dfrac{a\sqrt{15}}{3}=\dfrac{2a^3\sqrt{15}}{9}\end{aligned}$$
