Ngân hàng bài tập
A
Lăng trụ tam giác \(ABC.A'B'C'\) có thể tích bằng \(V\). Khi đó thể tích khối chóp \(A.BCC'B'\) bằng
| \(\dfrac{V}{3}\) | |
| \(\dfrac{2V}{3}\) | |
| \(\dfrac{3V}{4}\) | |
| \(\dfrac{V}{2}\) |
1 lời giải
Chọn phương án B.
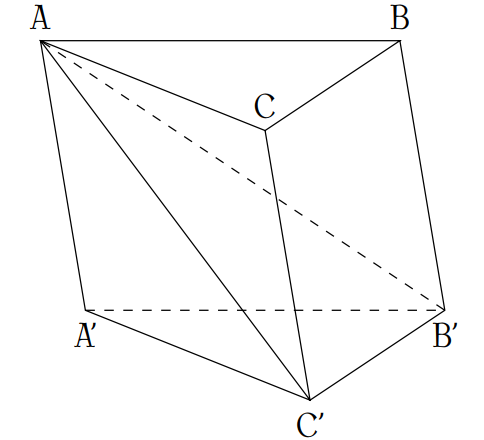
Gọi \(h\) là chiều cao của hình lăng trụ \(ABC.A'B'C'\), ta có \(h=\mathrm{d}\left(A,(A'B'C')\right)\) và \(V=S_{A'B'C'}\cdot h\).
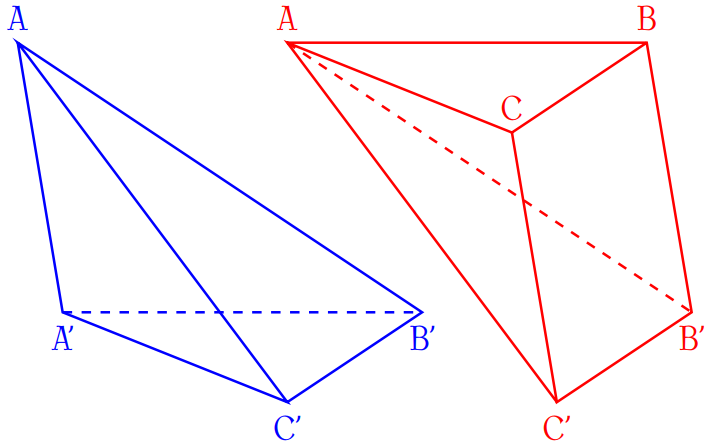
Xét khối chóp \(A.A'B'C'\) ta có $$V_{A.A'B'C'}=\dfrac{1}{3}S_{A'B'C'}\cdot h=\dfrac{V}{3}$$Do đó, khối chóp \(A.BCC'B'\) có thể tích bằng $$V-V_{A.A'B'C'}=V-\dfrac{V}{3}=\dfrac{2V}{3}$$
