Ngân hàng bài tập
S
Cho khối lăng trụ \(ABC.A'B'C'\) có thể tích bằng \(a^3\). Gọi \(M,\,N\) lần lượt là trung điểm của \(A'B'\) và \(CC'\). Tính thể tích khối chóp \(ABMN\).
| \(\dfrac{2a^3}{3}\) | |
| \(\dfrac{a^3}{3}\) | |
| \(\dfrac{a^3\sqrt{3}}{2}\) | |
| \(a^3\sqrt{3}\) |
1 lời giải
Chọn phương án B.
Gọi \(h\) là chiều cao của lăng trụ \(ABC.A'B'C'\).
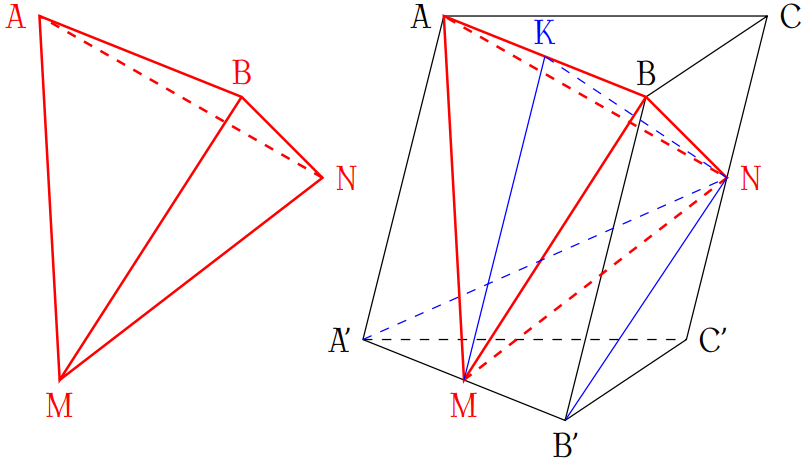
Ta có $$\begin{aligned}
V_{N.ABC}=V_{N.A'B'C'}&=\dfrac{1}{3}S_{ABC}\cdot\dfrac{h}{2}\\
&=\dfrac{1}{6}S_{ABC}\cdot h\\
&=\dfrac{V}{6}=\dfrac{a^3}{6}.
\end{aligned}$$
Khi đó khối chóp \(N.ABB'A'\) có thể tích bằng $$\begin{aligned}
V_{ABC.A'B'C'}-\left(V_{N.ABC}+V_{N.A'B'C'}\right)&=a^3-\left(\dfrac{a^3}{6}+\dfrac{a^3}{6}\right)\\
&=\dfrac{2}{3}a^3.
\end{aligned}$$
V_{ABC.A'B'C'}-\left(V_{N.ABC}+V_{N.A'B'C'}\right)&=a^3-\left(\dfrac{a^3}{6}+\dfrac{a^3}{6}\right)\\
&=\dfrac{2}{3}a^3.
\end{aligned}$$
Vậy thể tích khối hộp \(N.ABM\) là $$V_{N.ABM}=\dfrac{1}{2}V_{N.ABB'A'}=\dfrac{1}{2}\cdot\dfrac{2}{3}a^3=\dfrac{a^3}{3}.$$
