Ngân hàng bài tập
A
Đồ thị sau đây là của hàm số \(y=x^3-3x+1\).
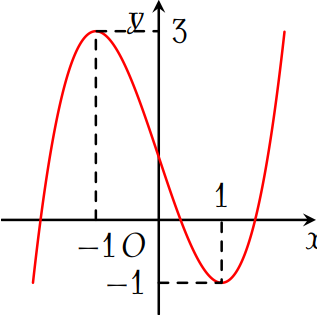
Với giá trị nào của \(m\) thì phương trình \(x^3-3x-m=0\) có \(3\) nghiệm phân biệt?
| \(-2< m<2\) | |
| \(-2< m<3\) | |
| \(-1< m<3\) | |
| \(-2\leq m<2\) |
1 lời giải
Chọn phương án A.
\(x^3-3x-m=0\Leftrightarrow x^3-3x+1=m+1\).
Phương trình \(x^3-3x+1=m+1\) có \(3\) nghiệm phân biệt khi và chỉ khi đường thẳng \(y=m+1\) cắt đường cong \(y=x^3-3x+1\) tại \(3\) điểm phân biệt.
Theo đồ thị ta thấy $$-1< m+1<3\Leftrightarrow-2< m<2$$
