Từ một tấm bìa hình vuông \(ABCD\) có cạnh bằng \(5\)dm, người ta cắt bỏ bốn tam giác bằng nhau \(AMB\), \(BNC\), \(CPD\), \(DQA\).
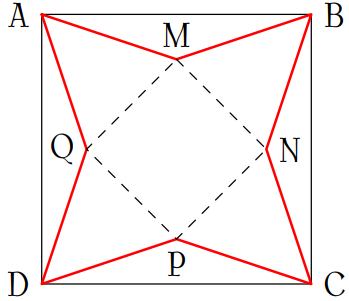
Với phần còn lại, người ta gắp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất?
| \(\dfrac{3\sqrt{2}}{2}\) | |
| \(\dfrac{5}{2}\) | |
| \(\dfrac{5\sqrt{2}}{2}\) | |
| \(2\sqrt{2}\) |
Chọn phương án D.
Theo hình vẽ, khối chóp dựng được là khối chóp \(A.MNPQ\), có đáy là hình vuông \(MNPQ\).
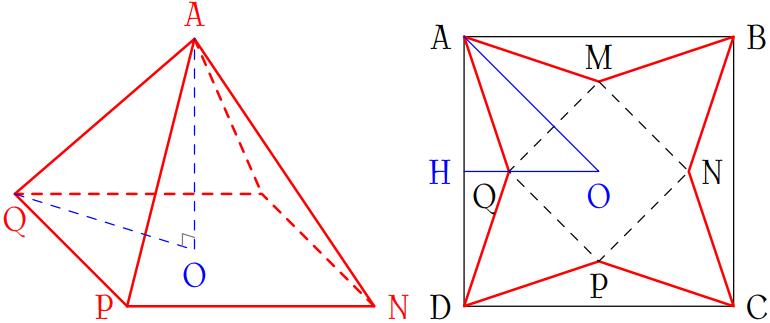
Gọi \(2x\) là chiều dài cạnh đáy hình vuông \(MNPQ\) (\(x>0\)), \(O\) là tâm của \(MNPQ\), \(H\) là trung điểm đoạn thẳng \(AD\).
Ta có \(QN=2x\sqrt{2}\Rightarrow OQ=x\sqrt{2}\).
Khi đó $$\begin{aligned}HQ&=OH-OQ\\ &=\dfrac{5}{2}-x\sqrt{2}\;\left(x<\dfrac{5\sqrt{2}}{4}\right)\end{aligned}$$
Xét tam giác vuông \(HAQ\) ta có $$\begin{aligned}AQ&=\sqrt{AH^2+HQ^2}\\ &=\sqrt{\left(\dfrac{5}{2}\right)^2+\left(\dfrac{5}{2}-x\sqrt{2}\right)^2}\\ &=\sqrt{\dfrac{50}{4}-5x\sqrt{2}+2x^2}\end{aligned}$$
Xét tam giác vuông \(AOQ\) ta có $$\begin{aligned}AO&=\sqrt{AQ^2-QO^2}\\ &=\sqrt{\left(\dfrac{50}{4}-5x\sqrt{2}+2x^2\right)-\left(x\sqrt{2}\right)^2}\\ &=\sqrt{\dfrac{50}{4}-5x\sqrt{2}}\end{aligned}$$
Đặt \(f(x)=x^2\sqrt{50-20x\sqrt{2}}\).
Ta có \(f'(x)=\dfrac{100x-50x^2\sqrt{2}}{\sqrt{50-20x\sqrt{2}}}\).
Cho \(f'(x)=0\Leftrightarrow\left[\begin{array}{ll}
x=0 &\text{(loại)}\\
x=\sqrt{2} &\text{(nhận)}
\end{array}\right.\)
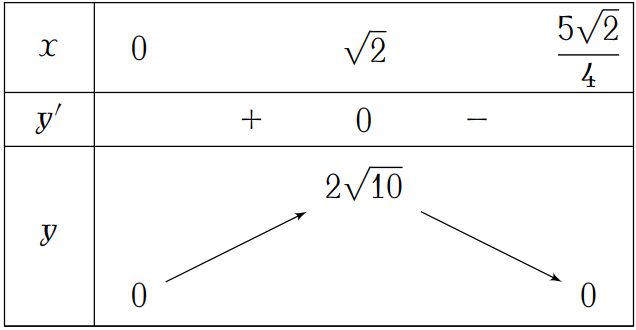
Theo đó, để khối chóp \(A.MNPQ\) có thể tích lớn nhất thì \(x=\sqrt{2}\).
Vậy cạnh đáy cần tìm bằng \(2x=2\sqrt{2}\).
