Ngân hàng bài tập
S
Biết hàm số \(f(x)=\dfrac{a}{b^2\cdot3^x}\) có đồ thị đối xứng với đồ thị hàm số \(y=3^x\) qua đường thẳng \(x=-1\). Biết \(a,\,b\) là các số nguyên.
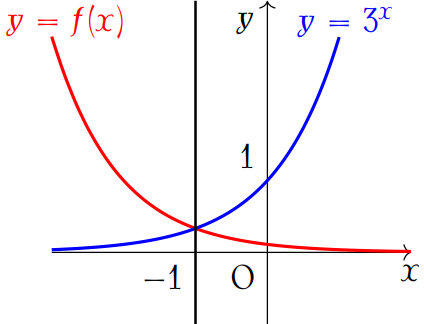
Chọn khẳng định đúng trong các khẳng định sau:
| \(b^2=9a\) | |
| \(b^2=4a\) | |
| \(b^2=6a\) | |
| \(b^2=a\) |
1 lời giải
Chọn phương án A.
Ta thấy hai đồ thị cắt nhau tại điểm có hoành độ \(x_0=-1\).
Khi đó \(y_0=3^{-1}=\dfrac{1}{3}\).
Thay vào \(f(x)\) ta được $$\begin{eqnarray*}
&\dfrac{1}{3}&=\dfrac{a}{b^2\cdot3^{-1}}=\dfrac{a}{b^2\cdot\dfrac{1}{3}}\\
\Leftrightarrow&\dfrac{1}{9}&=\dfrac{a}{b^2}\\
\Leftrightarrow&b^2&=9a.
\end{eqnarray*}$$
