Ngân hàng bài tập
A
Tiếp tuyến của đường cong \(\left(\mathscr{C}\right)\colon y=\dfrac{2x+1}{x-1}\) tại điểm \(M(2;5)\) cắt các trục tọa độ \(Ox\), \(Oy\) lần lượt tại \(A\) và \(B\). Tính diện tích tam giác \(OAB\).
| \(\dfrac{121}{6}\) | |
| \(\dfrac{121}{3}\) | |
| \(-\dfrac{121}{6}\) | |
| \(-\dfrac{121}{3}\) |
1 lời giải
Chọn phương án A.
Ta có \(y'=\dfrac{-3}{(x-1)^2}\).
Suy ra \(y'(2)=\dfrac{-3}{(2-1)^2}=-3\).
Vậy tiếp tuyến đã cho có phương trình là $$y=-3(x-2)+5=-3x+11.$$
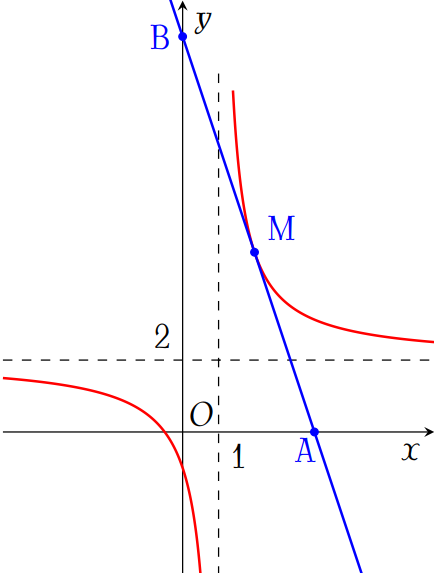
- Cho \(x=0\Rightarrow y=11\Rightarrow B(0;11)\)
- Cho \(y=0\Rightarrow x=\dfrac{11}{3}\Rightarrow A\left(\dfrac{11}{3};0\right)\)
Tam giác \(OAB\) vuông tại \(O\) và có \(OA=\dfrac{11}{3}\) và \(OB=11\).
Vậy \(S_{OAB}=\dfrac{1}{2}OA\cdot OB=\dfrac{1}{2}\cdot\dfrac{11}{3}\cdot11=\dfrac{121}{6}\).
