Ngân hàng bài tập
S
Tìm \(m\) để bất phương trình \(x+\dfrac{4}{x-1}\geq m\) có nghiệm trên khoảng \((-\infty;1)\).
| \(m\leq3\) | |
| \(m\leq-3\) | |
| \(m\leq5\) | |
| \(m\leq-1\) |
1 lời giải
Chọn phương án B.
Đặt \(f(x)=x+\dfrac{4}{x-1}\).
Tập xác định: \(\mathscr{D}=\mathbb{R}\setminus\{1\}\).
Ta có \(f'(x)=1-\dfrac{4}{(x-1)^2}=\dfrac{x^2-2x-3}{(x-1)^2}\).
Cho \(f'(x)=0\Leftrightarrow\left[\begin{array}{ll}
x=-1 &\in(-\infty;1)\\ x=3 &\notin(-\infty;1)
\end{array}\right.\)
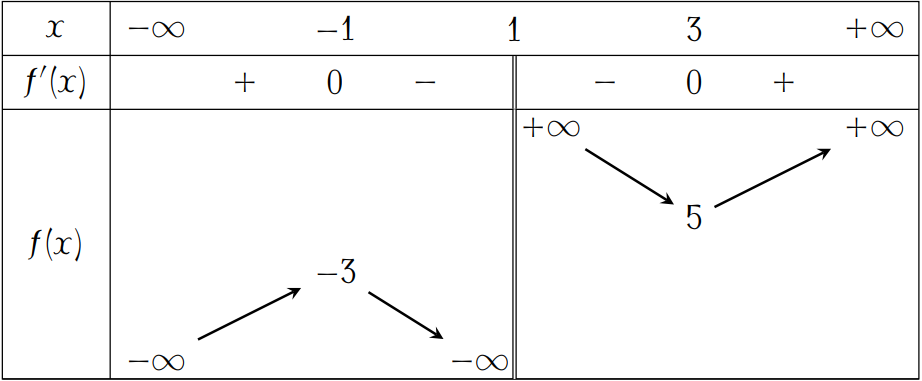
Suy ra giá trị lớn nhất của \(f(x)\) trên khoảng \((-\infty;1)\) là \(-3\).
Vậy để bất phương trình \(x+\dfrac{4}{x-1}\geq m\) có nghiệm trên khoảng \((-\infty;1)\) thì \(m\leq-3\).
