Ngân hàng bài tập: Lời giải

[Đề thi HK1 môn Toán 12 - Vĩnh Long (2020-2021)]

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SA=a$ và $SA$ vuông góc với đáy. Gọi $M$ là trung điểm của $SB$, $N$ thuộc cạnh $SD$ sao cho $SN=2ND$. Tính thể tích $V$ của khối tứ diện $ACMN$.

	$V=\dfrac{1}{12}a^3$
	$V=\dfrac{1}{36}a^3$
	$V=\dfrac{1}{8}a^3$
	$V=\dfrac{1}{6}a^3$

2 lời giải

Huỳnh Phú Sĩ

Trở lại Tương tự

Thêm lời giải

2 lời giải

Huỳnh Phú Sĩ

10:41 19/01/2021

Chọn phương án A.

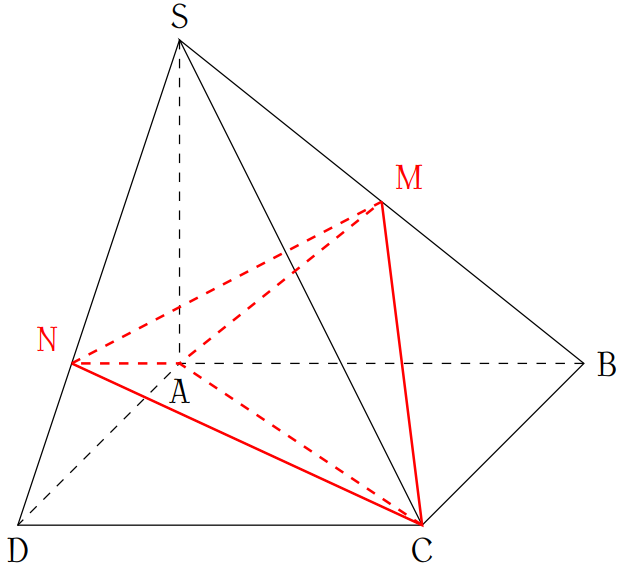
Vì các đường thẳng $AB$, $AD$, $AS$ đôi một vuông góc nên ta đặt hình chóp $S.ABCD$ vào hệ trục tọa độ $Oxyz$ sao cho $A\equiv O(0;0;0)$, $B\in Ox$, $D\in Oy$, $S\in Oz$.

Cho $a=1$ ta có $A(0;0;0)$, $B(1;0;0)$, $D(0;1;0)$, $C(1;1;0)$, $S(0;0;1)$, $M\left(\dfrac{1}{2};0;\dfrac{1}{2}\right)$, $N\left(0;\dfrac{2}{3};\dfrac{1}{3}\right)$.

Khi đó:

$\overrightarrow{AM}=\left(\dfrac{1}{2};0;\dfrac{1}{2}\right)$
$\overrightarrow{AN}=\left(0;\dfrac{2}{3};\dfrac{1}{3}\right)$
$\overrightarrow{AC}=(1;1;0)$
$\left[\overrightarrow{AM},\overrightarrow{AN}\right]=\left(-\dfrac{1}{3};-\dfrac{1}{6};\dfrac{1}{3}\right)$
$\left[\overrightarrow{AM},\overrightarrow{AN}\right]\cdot\overrightarrow{AC}=-\dfrac{1}{3}-\dfrac{1}{6}=-\dfrac{1}{2}$

Suy ra $\dfrac{1}{6}\left|\left[\overrightarrow{AM},\overrightarrow{AN}\right]\cdot\overrightarrow{AC}\right|=\dfrac{1}{6}\cdot\dfrac{1}{2}=\dfrac{1}{12}$.

Vậy $V_{ACMN}=\dfrac{a^3}{12}$.

Huỳnh Phú Sĩ

10:35 19/01/2021

Chọn phương án A.

Ta có $V_{S.ABCD}=\dfrac{1}{3}S_{ABCD}\cdot SA=\dfrac{1}{3}a^2\cdot a=\dfrac{a^3}{3}$.

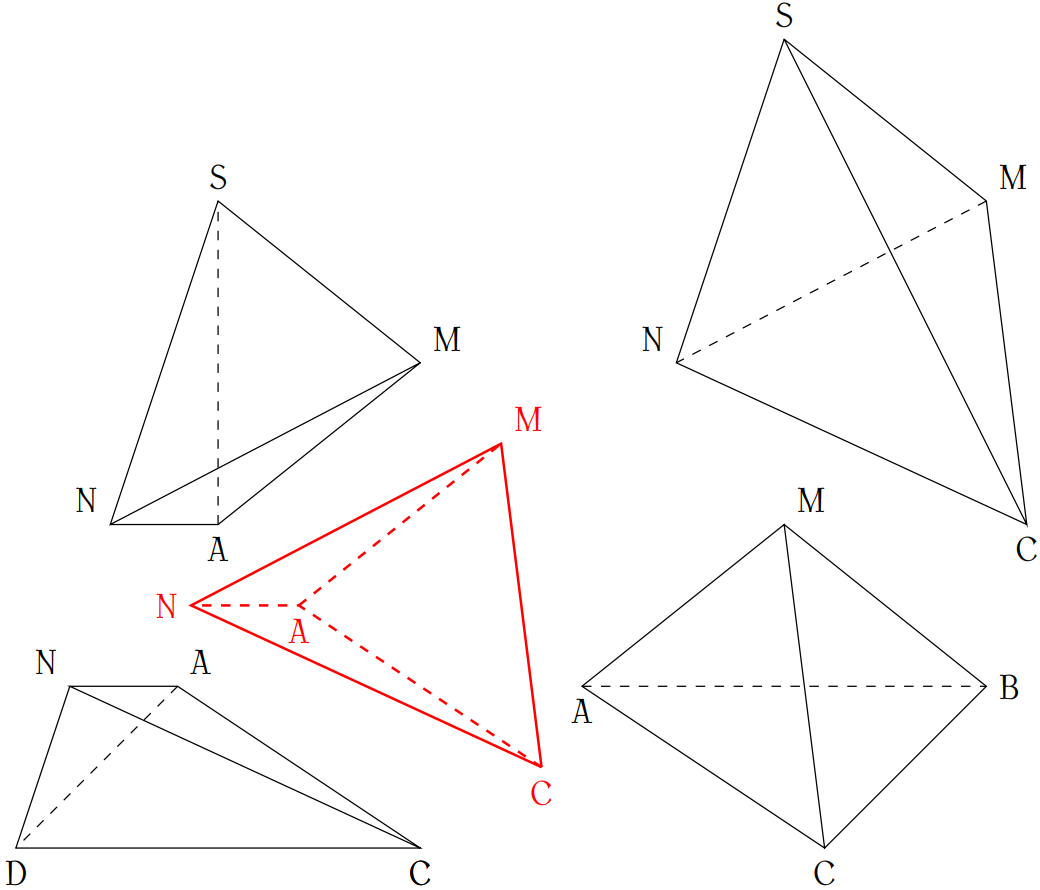
Ta thấy $$V_{S.ABCD}=V_{ACMN}+V_{SAMN}+V_{MABC}+V_{NADC}+V_{SCMN}$$

Ngoài ra, vì $ABCD$ là hình vuông cạnh $a$ nên $$\begin{aligned}V_{S.ABC}=V_{S.ACD}=V_{S.ABD}=V_{S.BCD}&=\dfrac{1}{2}V_{S.ABCD}\\ &=\dfrac{a^3}{6}\end{aligned}$$

$\blacksquare$ Xét hình chóp $S.ABC$ ta có $$\begin{aligned}
\dfrac{V_{S.AMC}}{V_{S.ABC}}&=\dfrac{SA}{SA}\cdot\dfrac{SM}{SB}\cdot\dfrac{SC}{SC}=\dfrac{1}{2}\\
\Rightarrow V_{S.AMC}&=\dfrac{1}{2}V_{S.ABC}\\
\Rightarrow V_{MABC}&=\dfrac{1}{2}V_{S.ABC}=\dfrac{1}{2}\cdot\dfrac{a^3}{6}=\dfrac{a^3}{12}\;(1)
\end{aligned}$$
$\blacksquare$ Xét hình chóp $S.ABD$ ta có $$\begin{aligned}
\dfrac{V_{S.AMN}}{V_{S.ABD}}&=\dfrac{SA}{SA}\cdot\dfrac{SM}{SB}\cdot\dfrac{SN}{SD}=\dfrac{1}{2}\cdot\dfrac{2}{3}=\dfrac{1}{3}\\
\Rightarrow V_{SAMN}&=\dfrac{1}{3}V_{S.ABD}=\dfrac{1}{3}\cdot\dfrac{a^3}{6}=\dfrac{a^3}{18}\;(2)
\end{aligned}$$
$\blacksquare$ Xét hình chóp $S.ACD$ ta có $$\begin{aligned}
\dfrac{V_{S.ACN}}{V_{S.ACD}}&=\dfrac{SA}{SA}\cdot\dfrac{SC}{SC}\cdot\dfrac{SN}{SD}=\dfrac{2}{3}\\
\Rightarrow V_{S.ACN}&=\dfrac{2}{3}V_{S.ABC}\\
\Rightarrow V_{NACD}&=\dfrac{1}{3}V_{S.ACD}=\dfrac{1}{3}\cdot\dfrac{a^3}{6}=\dfrac{a^3}{18}\;(3)
\end{aligned}$$
$\blacksquare$ Xét hình chóp $S.BCD$ ta có $$\begin{aligned}
\dfrac{V_{S.CMN}}{V_{S.CBD}}&=\dfrac{SC}{SC}\cdot\dfrac{SM}{SB}\cdot\dfrac{SN}{SD}=\dfrac{1}{2}\cdot\dfrac{2}{3}=\dfrac{1}{3}\\
\Rightarrow V_{SCMN}&=\dfrac{1}{3}V_{S.CBD}=\dfrac{1}{3}\cdot\dfrac{a^3}{6}=\dfrac{a^3}{18}\;(4)
\end{aligned}$$

Vậy khối tứ diện $ACMN$ có thể tích là $$\begin{aligned}
V_{ACMN}&=V_{S.ABCD}-\left(V_{SAMN}+V_{MABC}+V_{NADC}+V_{SCMN}\right)\\
&=\dfrac{a^3}{8}-\left(\dfrac{a^3}{18}+\dfrac{a^3}{12}+\dfrac{a^3}{18}+\dfrac{a^3}{18}\right)\\
&=\dfrac{a^3}{12}.
\end{aligned}$$

	\(V=\dfrac{1}{12}a^3\)
	\(V=\dfrac{1}{36}a^3\)
	\(V=\dfrac{1}{8}a^3\)
	\(V=\dfrac{1}{6}a^3\)