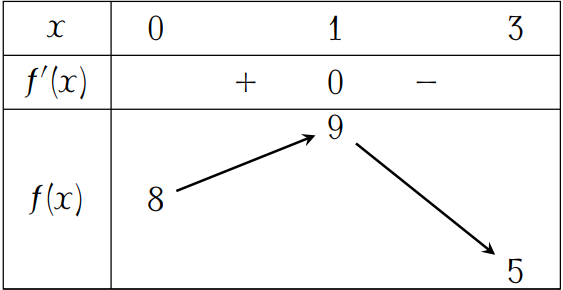
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Gọi \(S\) là tập hợp các số nguyên dương \(m\) để bất phương trình $$f(x)\geq mx^2\left(x^2-2\right)+2m$$có nghiệm thuộc đoạn \([0;3]\). Số phần tử của tập \(S\) là
| \(9\) | |
| \(10\) | |
| Vô số | |
| \(0\) |
Chọn phương án A.
Bất phương trình đã cho tương đương với $$\dfrac{f(x)}{x^4-2x^2+2}\geq m$$
Đặt \(g(x)=\dfrac{f(x)}{x^4-2x^2+2}\).
Ta có $$g'(x)=\dfrac{\left(x^4-2x^2+2\right)f'(x)-\left(4x^3-4x\right)f(x)}{\left(x^4-2x^2+2\right)^2}$$
\(\blacksquare\) Trên khoảng \((0;1)\) ta có
- \(f'(x)>0\)
- \(x^4-2x^2+2=\left(1-x^2\right)^2+1>0\)
- \(f(x)>0\)
- \(4x^3-4x=4x\left(x^2-1\right)<0\)
\(\Rightarrow\left(x^4-2x^2+2\right)f'(x)-\left(4x^3-4x\right)f(x)>0\)
\(\Rightarrow g'(x)>0\).
\(\blacksquare\) Trên khoảng \((1;3)\) ta có
- \(f'(x)<0\)
- \(x^4-2x^2+2=\left(x^2-1\right)^2+1>0\)
- \(f(x)>0\)
- \(4x^3-4x=4x\left(x^2-1\right)>0\)
\(\Rightarrow\left(x^4-2x^2+2\right)f'(x)-\left(4x^3-4x\right)f(x)<0\)
\(\Rightarrow g'(x)<0\).

Để bất phương trình \(g(x)\geq m\) có nghiệm trên đoạn \([0;3]\) thì \(m\leq9\).
Vì \(m\) nguyên dương nên $$m\in\left\{1;2;3;4;5;6;7;8;9\right\}$$
Vậy tập \(S\) cần tìm có \(9\) phần tử.
