Trong không gian \(Oxyz\), cho mặt cầu \(\left(S\right)\colon\left(x-2\right)^2+\left(y-1\right)^2+\left(z-1\right)^2=9\) và \(M\left(x_0;y_0;z_0\right)\in\left(S\right)\) sao cho \(A=x_0+2y_0+2z_0\) đạt giá trị nhỏ nhất. Khi đó \(x_0+y_0+z_0\) bằng
| \(2\) | |
| \(-1\) | |
| \(-2\) | |
| \(1\) |
Chọn phương án B.
Mặt cầu \(\left(S\right)\colon\left(x-2\right)^2+\left(y-1\right)^2+\left(z-1\right)^2=9\) có tâm \(I(2;1;1)\) và bán kính \(R=3\).
Xét mặt phẳng \((\alpha)\colon x+2y+2z=0\).
Gọi \(N\) là hình chiếu vuông góc của điểm \(M\) trên mặt phẳng \((\alpha)\).
Ta có $$\begin{aligned}\mathrm{d}\left(M,(\alpha)\right)=MN&=\dfrac{\left|x_0+2y_0+2z_0\right|}{\sqrt{1^2+2^2+2^2}}\\ &=\dfrac{\left|x_0+2y_0+2z_0+d\right|}{3}\end{aligned}$$
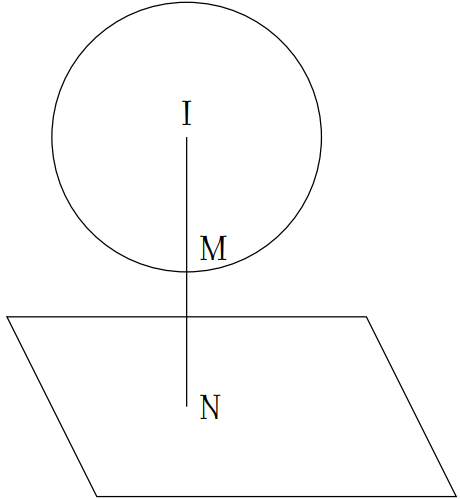
Gọi \(\Delta\) là đường thẳng đi qua ba điểm \(I,\,M,\,N\). Khi đó \(\Delta\) đi qua \(I(2;1;1)\) và vuông góc với \((\alpha)\) nên nhận vectơ \(\overrightarrow{n}=(1;2;2)\) làm vectơ chỉ phương. $$\Delta\colon\begin{cases}
x=2+t\\ y=1+2t\\ z=1+2t
\end{cases}$$
Thay vào phương trình \(\left(x-2\right)^2+\left(y-1\right)^2+\left(z-1\right)^2=9\) ta được $$\begin{aligned}
&\left(2+t-2\right)^2+\left(1+2t-1\right)^2+\left(1+2t-1\right)^2=9\\
\Leftrightarrow&\,t^2+4t^2+4t^2=9\\
\Leftrightarrow&\,t^2=1\\
\Leftrightarrow&\left[\begin{array}{l}
t=1\\ t=-1
\end{array}\right.\\
\Leftrightarrow&\left[\begin{array}{l}
M(3;3;3)\\ M(1;-1;-1)
\end{array}\right.
\end{aligned}$$
- Với \(M(3;3;3)\): \(A=3+2\cdot3+2\cdot3=15\).
- Với \(M(1;-1;-1)\): \(A=1+2\cdot(-1)+2\cdot(-1)=-3\).
Vậy \(M(1;-1;-1)\) là điểm cần tìm.
Do đó \(x_0+y_0+z_0=1-1-1=-1\).
