Ngân hàng bài tập
B
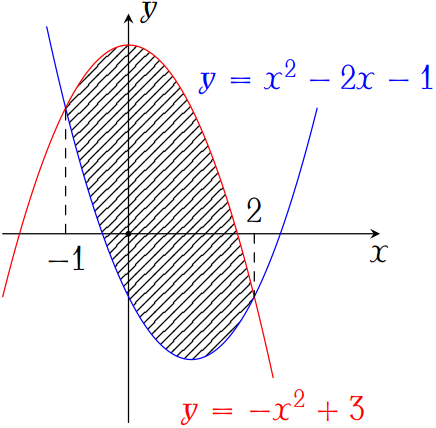
Diện tích phần hình phẳng gạch chéo trong hình vẽ trên được tính theo công thức nào dưới đây?
| \(\displaystyle\int\limits_{-1}^{2}(-2x+2)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{-1}^{2}(2x-2)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{-1}^{2}\left(-2x^2+2x+4\right)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{-1}^{2}\left(2x^2-2x-4\right)\mathrm{\,d}x\) |
1 lời giải
Chọn phương án C.
Theo hình vẽ ta thấy $$\begin{aligned}S&=\displaystyle\int\limits_{-1}^{2}\left(\left[-x^2+3\right]-\left[x^2-2x-1\right]\right)\mathrm{\,d}x\\ &=\displaystyle\int\limits_{-1}^{2}\left(-2x^2+2x+4\right)\mathrm{\,d}x.\end{aligned}$$
